| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 백준
- Direct12
- 타입 객체
- 멀티프로세서
- 디자인패턴
- 자료구조
- 스케줄링
- DirectX 12
- 파일시스템 구현
- 병행성
- 프로그래머스
- 렌더링 파이프라인
- 동적계획법
- 영속성
- 락
- 병행성 관련 오류
- directx
- I/O장치
- OS
- 운영체제
- 다이나믹 프로그래밍
- 알고리즘
- DirectX12
- 그리디 알고리즘
- 멀티쓰레드
- 쓰레드
- codility
- 다이나믹프로그래밍
- 컨디션 변수
- 그리디알고리즘
Archives
- Today
- Total
기록공간
타일 장식물 (프로그래머스) 본문
반응형
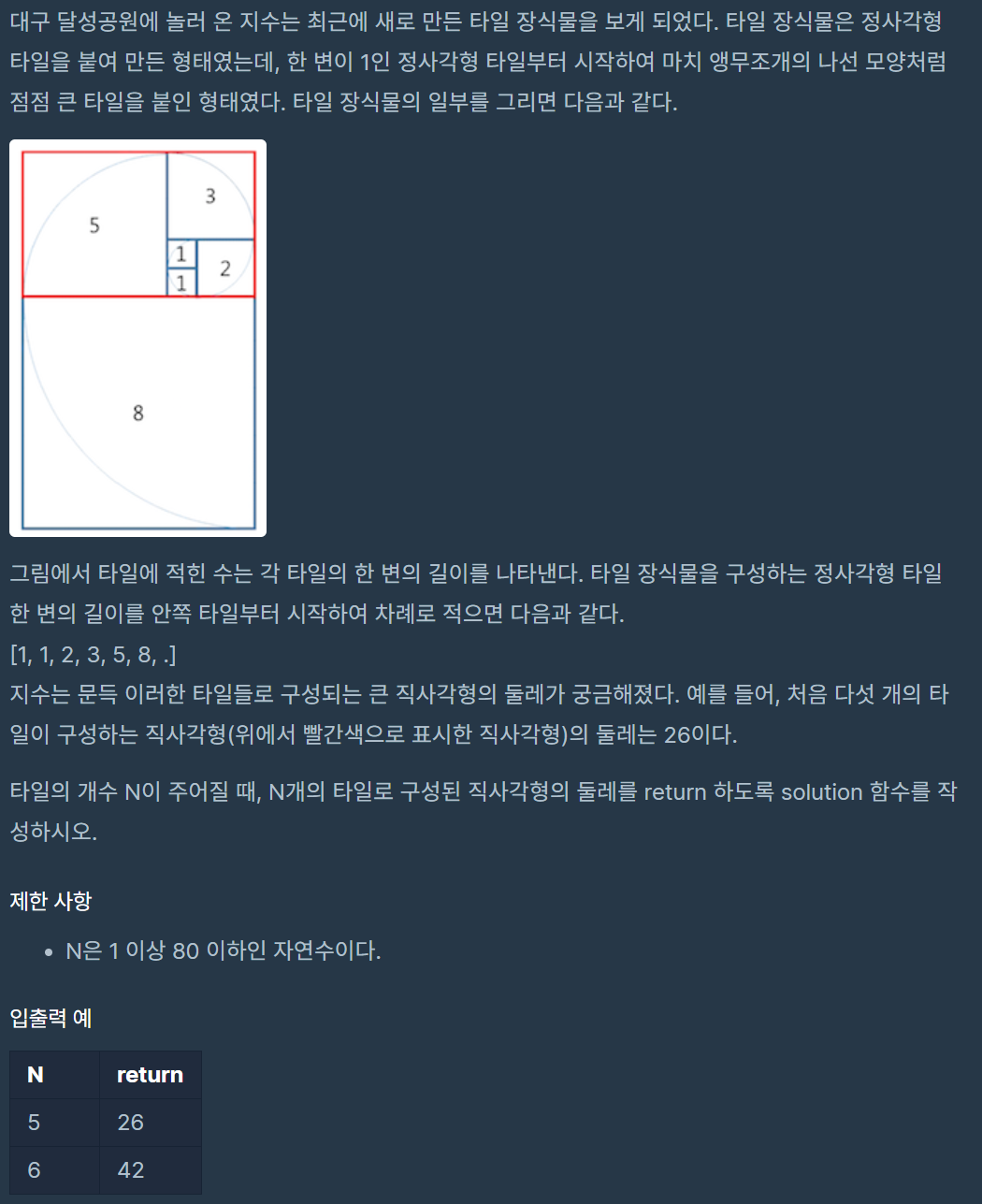
한 변의 길이를 알기 위해서는 우선 타일의 수가 어떻게 되는지 먼저 살펴봐야 한다.
1, 1, 2, 3, 5, 8, ...
규칙을 제대로 살펴보면 3번째 값부터 1번째 2번째 값을 합한 값이 나온다. 점화식으로 표현하면 다음과 같다.
D[i] = D[i - 2] + D[i - 1] (i >= 3)
타일의 수는 이전 값을 기반으로 하여 구하기 때문에 동적 계획법을 사용하여야 한다. 이렇게 타일의 수들을 구했다면 타일 개수에 맞는 직사각형의 둘레를 구할 수 있게 된다. 어떻게 구하면 될까?

위 문제에서는 5개의 타일로 구성된 직사각형의 둘레를 구하는것을 그림으로 표현하였다. 그림을 살펴보면 5개의 타일들 중 가장 나중과 그 이전 타일만 안다면 직사각형 각 변의 길이를 구할 수 있게 된다.

모든 변의 길이를 더하면 그것이 직사각형의 둘레이므로 이 예제의 직사각형 둘레는 26이다. 직사각형의 둘레를 구하는 것을 수식으로 표현하면 다음과 같다.
직사각형의 둘레 = (D[N번째 타일] + D[N-1번째 타일]) * 2 + D[N번째 타일] * 2
= (D[N번째 타일] + D[N번째 타일] + D[N-1번째 타일]) * 2
코드로 표현하면 다음과 같다.
#include <vector>
using namespace std;
long long solution(int N)
{
vector<long long> d;
d.assign(80, 0); // 1 ~ 80까지 범위이므로 미리 할당한다.
d[0] = 1; d[1] = 1; // 점화식 계산을 위해 1, 2번째 타일 값을 미리 대입한다.
for(int i = 2; i < N; ++i) d[i] = d[i - 2] + d[i - 1];
return (d[N - 1] + d[N - 1] + d[N - 2]) * 2;
}
반응형
'Algorithm > 문제' 카테고리의 다른 글
| 디스크 컨트롤러 (프로그래머스) (0) | 2020.05.20 |
|---|---|
| 라면공장 (프로그래머스) (0) | 2020.05.20 |
| 비밀지도 (프로그래머스) (0) | 2020.05.16 |
| 크레인 인형뽑기 게임 (프로그래머스) (0) | 2020.05.16 |
| 베스트앨범 (프로그래머스) (0) | 2020.05.11 |
Comments




