| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 디자인패턴
- 알고리즘
- 그리디 알고리즘
- 스케줄링
- 프로그래머스
- 멀티프로세서
- 동적계획법
- 파일시스템 구현
- 락
- 컨디션 변수
- DirectX12
- 운영체제
- 쓰레드
- directx
- codility
- 다이나믹프로그래밍
- 병행성 관련 오류
- DirectX 12
- 렌더링 파이프라인
- 자료구조
- 다이나믹 프로그래밍
- 병행성
- 그리디알고리즘
- I/O장치
- Direct12
- 멀티쓰레드
- 타입 객체
- 백준
- 영속성
- OS
Archives
- Today
- Total
기록공간
가장 큰 정사각형 찾기 (프로그래머스) 본문
반응형
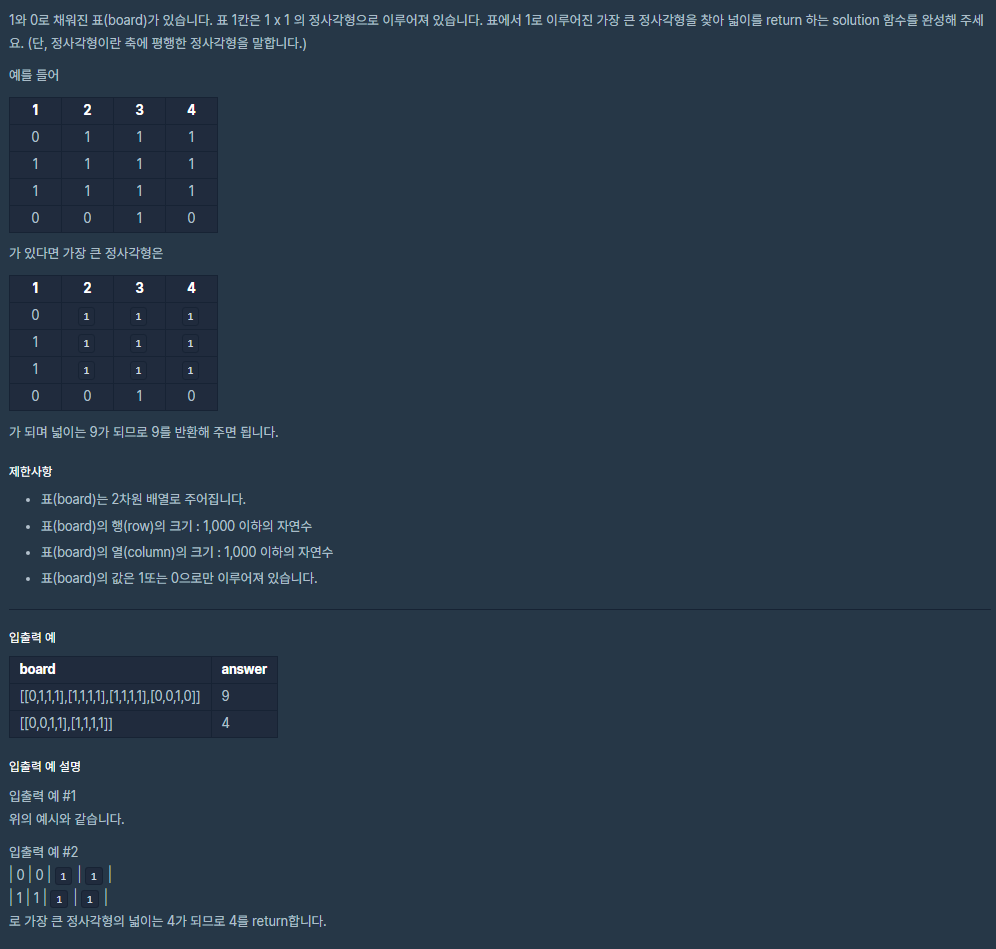
우선 처음 생각해 볼 수 있는 방법은 반복문을 사용하여 모든 위치를 검사하며 그 위치로부터 정사각형이 되는 범위를 찾는 것이다. 하지만 이 방법의 시간 복잡도는 O(n^3)로 만약 행과 열의 크기가 1000이라면 최악의 경우 1000 * 1000 * 1000 = 1000000000으로 효율성 테스트를 통과할 수 없게 된다.
이런 이유로 동적 계획법을 활용하여야 한다. 동적 계획법의 사용 방법은 다음과 같다.
우선 표의 정보를 모두 동적 테이블에 담아 놓는다. 그리고 다음 과정을 반복한다.

동적 테이블 위치는 [1, 1] 부터 시작한다. 이 위치에서 왼쪽, 위쪽, 왼쪽 위쪽(대각선) 값들 중 가장 작은 값 min을 찾는다. 그리고 min + 1을 하면 해당 위치에서의 정사각형 넓이가 된다. 그 값을 현재 위치에 갱신해주면 된다. 이후 값들은 이전에 기록해놓은 테이블 정보를 사용하면 더 빠르게 넓이를 구할 수 있게 된다.
코드는 다음과 같다.
#include<vector>
using namespace std;
// 3개의 값중 가장 작은 값을 찾는 함수
int MIN(int a, int b, int c)
{
return a > b ? (b > c) ? c : b : (a > c) ? c : a;
}
int solution(vector<vector<int>> board)
{
// 길이가 1x1인 경우가 있을 수 있으므로
// board의 맨 처음 값을 answer로 선언해준다.
int answer = board[0][0];
// 동적 테이블 생성 및 할당
vector<vector<int>> dp(board.size());
for(int i = 0; i < dp.size(); ++i) dp[i].assign(board[0].size(), 0);
// board 정보를 테이블에 복사한다.
for(int i = 0; i < board.size(); ++i)
{
for(int j = 0; j < board[0].size(); ++j)
{
dp[i][j] = board[i][j];
}
}
// [1, 1] 부터 [가로끝, 세로끝]까지 반복한다.
for(int i = 1; i < board.size(); ++i)
{
for(int j = 1; j < board[0].size(); ++j)
{
// 0인 경우 정사각형이 되는 조건을 만족하지 않으므로 넘어간다.
if(dp[i][j] == 0) continue;
else
{
// 왼, 오, 왼오 중 가장 작은 값을 찾는다.
int min = MIN(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]);
// 넓이 값을 테이블에 기록한다.
dp[i][j] = min + 1;
// 가장 큰 길이라면 answer값을 갱신한다.
if(answer < dp[i][j]) answer = dp[i][j];
}
}
}
return answer * answer;
}반응형
'Algorithm > 문제' 카테고리의 다른 글
| 올바른 괄호 (프로그래머스) (0) | 2020.06.12 |
|---|---|
| 카펫 (프로그래머스) (0) | 2020.06.12 |
| 숫자 야구 (프로그래머스) (0) | 2020.06.09 |
| 프린터 (프로그래머스) (0) | 2020.06.05 |
| 주식가격 (프로그래머스) (0) | 2020.06.05 |
Comments




