| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 컨디션 변수
- I/O장치
- 다이나믹 프로그래밍
- 디자인패턴
- 백준
- 스케줄링
- 그리디알고리즘
- Direct12
- 타입 객체
- 쓰레드
- directx
- codility
- 파일시스템 구현
- OS
- 멀티프로세서
- 병행성
- 자료구조
- DirectX 12
- 락
- 렌더링 파이프라인
- 다이나믹프로그래밍
- 운영체제
- 영속성
- DirectX12
- 동적계획법
- 알고리즘
- 멀티쓰레드
- 그리디 알고리즘
- 병행성 관련 오류
- 프로그래머스
Archives
- Today
- Total
기록공간
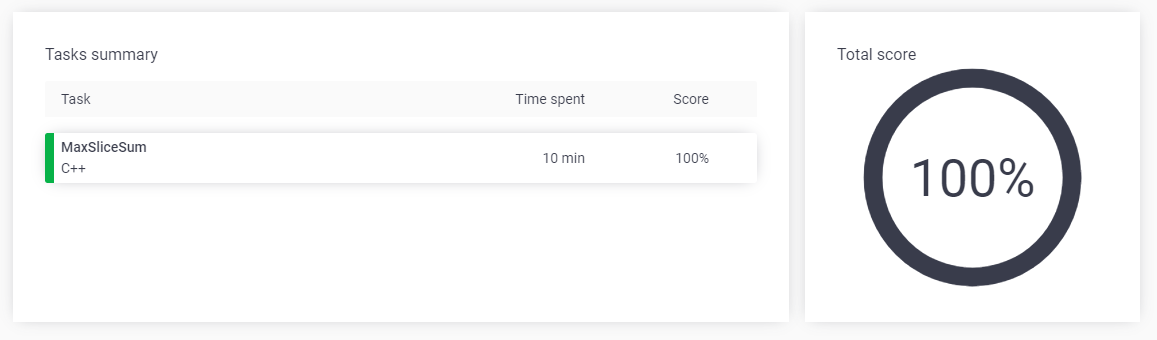
MaxSliceSum (Codility) 본문
반응형

문제
비어있지 않은 배열 N개의 정수를 담는 A가 주어진다. 0 <= P <= Q < N 범위를 만족하는 (P, Q)에서 A[P] + A[P+1] + ... + A[Q] 의 값을 slice라고 한다. 이 slice 값중 가장 큰 값을 구하는 프로그램을 작성하라
해결 방법
이전에 봤던 DoubleMaxSlice 문제와 비슷하다. 다음 예제를 통해 문제를 해결해보자.
A[0] A[1] A[2] A[3] A[4]
-3 2 6 4 1
우선 처음부터 값을 더해 나간다. 해당 인덱스에서 더한 값은 컨테이너 v에 저장한다.
sum 값을 이용해 더한 값을 기록한다. (sum은 0으로 초기화한다)
A[i] + sum 과 A[i] 중 더 큰 값을 v[i] 컨테이너에 저장하고 sum에 기록한다.
A[i]가 더 큰 경우는 지금까지 더했던 값들보다 현재 인덱스 값이 큰것으로, 현재 인덱스 위치부터 더하는 것이 더 slice값이 큰 것을 의미한다.
* v[0]
A[0](-3)과 sum(0) + A[0](-3)을 비교해 더 큰 값을 저장한다.
둘 다 같으므로 v[0]은 -3이다. sum은 -3이다.
* v[1]
A[1](2)과 sum(-3) + A[1](2)을 비교해 더 큰 값을 저장한다.
A[1]이 더 크므로 v[1]은 2이다. sum은 2이다.
* v[2]
A[2](6)과 sum(2) + A[2](6)을 비교해 더 큰 값을 저장한다.
sum(2) + A[2](6)이 더 크므로 v[2]은 8이다. sum은 8이다.
* v[3]
A[3](4)과 sum(8) + A[3](4)을 비교해 더 큰 값을 저장한다.
sum(8) + A[3](4)이 더 크므로 v[3]은 12이다. sum은 12이다.
* v[4]
A[4](1)과 sum(12) + A[4](1)을 비교해 더 큰 값을 저장한다.
sum(12) + A[4](1)이 더 크므로 v[4]은 13이다. sum은 13이다.
v[0] v[1] v[2] v[3] v[4]
-3 2 8 12 13
이 값들 중 가장 큰 값이 답이 된다.
v[4]가 제일 크므로 답은 13이다.
즉 (P, Q) = (1, 4) 이므로 (1 ~ 4) 인덱스 범위의 값들을 더한게 slice값이 된다.
코드는 다음과 같다.
#include <algorithm>
int max(const int& a, const int& b) {
return (a < b) ? b : a;
}
int solution(vector<int>& A) {
vector<int> v;
int sum = 0;
for(const auto& iter : A) {
sum = max(sum + iter, iter);
v.push_back(sum);
}
sort(v.begin(), v.end(), Greater<int>());
return v[0];
}

반응형
'Algorithm > 문제' 카테고리의 다른 글
| MinPerimeterRectangle (Codility) - Java (0) | 2020.08.18 |
|---|---|
| CountFactors (Codility) (0) | 2020.08.11 |
| MaxProfit (Codility) - Java (0) | 2020.08.01 |
| MaxDoubleSliceSum (Codility) - Java (2) | 2020.07.31 |
| EquiLeader (Codility) - Java (0) | 2020.07.29 |
Comments




