| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 멀티쓰레드
- 쓰레드
- I/O장치
- 운영체제
- 그리디알고리즘
- 다이나믹프로그래밍
- DirectX 12
- 자료구조
- 그리디 알고리즘
- 프로그래머스
- Direct12
- 디자인패턴
- 병행성 관련 오류
- 스케줄링
- DirectX12
- 파일시스템 구현
- 다이나믹 프로그래밍
- 백준
- 동적계획법
- directx
- 락
- 타입 객체
- 컨디션 변수
- codility
- OS
- 알고리즘
- 렌더링 파이프라인
- 병행성
- 멀티프로세서
- 영속성
- Today
- Total
기록공간
이진탐색트리 (Binary search tree) 본문
컴퓨터의 탐색은 레코드(Record)의 집합에서 특정한 레코드를 찾아내는 작업을 말한다. 레코드는 하나 이상의 필드(Field)로 구성된다.
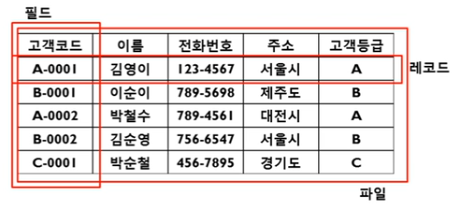
예를 들어, 각 학생의 정보를 이진트리의 각 노드에 저장한다고 생각해 보자. 학생정보 구조체가 레코드에 해당하고, 구조체의 멤버 변수인 학번, 이름, 주소, 주민등록번호 등이 필드에 해당한다. 레코드를 서로 구별하려면 필드들 중에서 서로 중복되지 않는 고유한 값을 가지는 필드가 있어야 하는데, 이를 키(Key)라고 부른다. 학생 정보에서는 주민등록번호나 학번이 여기에 해당된다. 결국 탐색은 주어진 키를 가진 레코드를 찾는 작업이고, 레코드가 노드에 저장되는 이진탐색트리에서는 주어진 키를 가진 노드를 찾아야 한다.
이진탐색트리의 정의
이진탐색트리(BST, Binary Search Tree)는 효율적인 탐색을 위한 이진트리 기반의 자료구조이다. 이진탐색트리는 다음과 같은 규칙이 존재한다.
-
모든 노드는 유일한 키를 갖는다.
-
왼쪽 서브 트리 키들은 루트 키보다 작다.
-
오른쪽 서브 트리 키들은 루트 키보다 크다.
-
왼쪽과 오른쪽 서브 트리도 이진탐색트리이다.
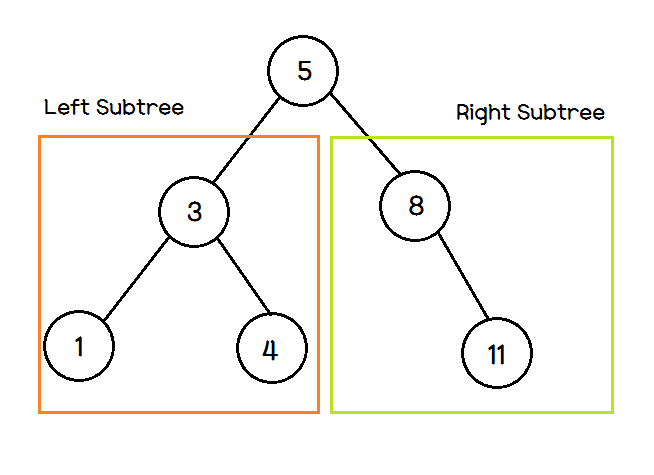
위 그림의 트리는 모든 노드가 이진탐색트리의 조건을 만족한다. 이 트리를 중위 순회 방법으로 순회하면 1, 3, 4, 5, 8, 11과 같이 숫자의 오름차순으로 노드를 방문한다.
모든 이진탐색트리는 이러한 성질을 갖는데, 따라서 어느 정도 정렬된 상태를 유지하고 있다고 볼 수 있다.
이진탐색트리의 연산
이진탐색트리는 이진트리의 일종이므로 기본적인 연산은 이진트리와 동일하다. 추가적인 데이터를 필요로 하지도 않는다. 앞서 소개했던 이진트리의 연산들을 그대로 사용할 수 있다.
선형 자료구조와는 달리 트리에서는 삽입과 삭제를 위해 노드의 위치를 정하는 것이 쉽지 않다. 그러나 이진탐색트리에서는 이 연산들을 구체화 할 수 있다. 이진탐색트리에서는 삽입(Insert), 삭제(Delete)와 탐색(Search) 연산에 집중하겠다. 이 연산들은 모두 이진탐색트리의 조건을 유지하면서 처리되어야 한다.
탐색 연산
이진탐색트리에서 키값으로 Key를 가진 노드를 탐색하려고 한다. 탐색은 항상 루트노드에서 시작하는데, 루트노드와의 비교 결과는 다음 세 가지 중의 하나이다.
-
Key가 루트의 키값과 같으면 루트가 찾는 노드이다. 탐색에 성공하였다.
-
Key가 루트의 키값보다 작으면 찾는 노드는 왼쪽 서브트리에 있다. 탐색을 루트의 왼쪽 자식을 기준으로 다시 시작한다.
-
Key가 루트의 키값보다 크면 찾는 노드는 오른쪽 서브트리에 있다. 탐색을 루트의 오른쪽 자식을 기준으로 다시 시작한다.
루트 아래의 노드에서도 같은 과정을 되풀이한다. 다음 그림은 이진탐색트리에서 11을 찾는 과정을 보여준다.
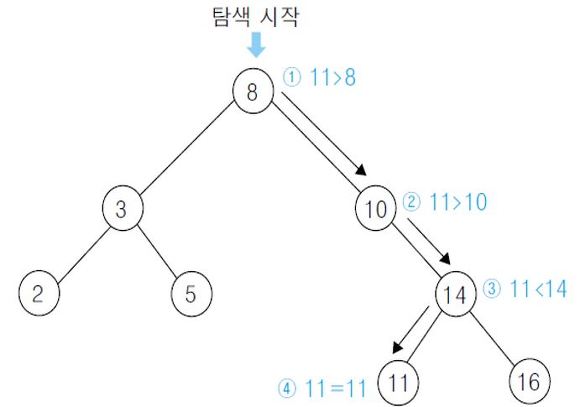
코드로 구현하면 다음과 같다.
NODE* Search(NODE* n, int key)
{
if (nullptr == n) // 노드에 동일한 키가 없으므로 탐색에 실패
return nullptr;
else if (n->data == key) // 노드에 키와 동일하다면 값을 찾은것
return n;
else if (n->data > key)
return Search(n->left, key); // 키가 노드보다 작은경우 왼쪽서브트리에서 찾는다.
else
return Search(n->right, key); // 키가 노드보다 큰경우 오른쪽서브트리에서 찾는다.
}반복적인 방법으로도 구현이 가능하다. 효율성으로만 따진다면 반복적인 함수가 더 우수하다.
NODE* Search(NODE* n, int key)
{
while (nullptr != n)
{
if (n->data == key)
return n;
else if (n->data > key)
n = node->left;
else
n = node->right;
}
return nullptr;
}이진탐색 트리는 키값을 기준으로 정렬되어 있다. 그렇다면 키가 아닌 다른 필드를 이용한 탐색은 가능할까? 가능은 하지만 탐색의 효율은 떨어진다. 일반적인 순회 알고리즘을 사용하여 모든 노드를 순서대로 검사해야하기 때문이다.
삽입 연산
이진탐색트리에서 노드를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요하다. 이유는 이진탐색트리에서는 같은 키 값을 갖는 노드가 없어야하고 또한 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치가 되기 때문이다.

위 그림은 노드 11을 이진탐색트리에 삽입하는 과정을 보여준다. 먼저 루트에서부터 11을 탐색한다. 만약 탐색이 성공한다면 이미 11이 트리 안에 존재하는 것이고, 키가 중복되므로 삽입이 불가능하다. 만약 11이 트리 안에 없으면 어디선가 탐색이 실패로 끝날 것이다. 실패한 위치가 11이 있어야 할 곳이다. 따라서 탐색이 실패로 끝난 위치인 19의 왼쪽에 삽입하면 된다.
코드로 구현하면 다음과 같다.
bool Insert(NODE* r, NODE* n)
{
if (n->data == r->data)
return false; // 이미 동일한 키가 존재하므로 삽입불가능(탐색 성공)
else if (n->data < r->data)
{
if (nullptr == r->left)
r->left = n; // 탐색에 실패한 위치에 새로운 노드 삽입
else
Insert(r->left, n); // 아직 찾아야 할 서브트리가 남아있음
}
else
{
if (nullptr == r->right)
r->right = n; // 탐색에 실패한 위치에 새로운 노드 삽입
else
Insert(r->right, n); // 아직 찾아야 할 서브트리가 남아있음
}
return true;
}
삭제 연산
노드를 삭제하는 것은 이진탐색트리에서 가장 복잡한 연산이다. 노드 삭제 후에도 이진탐색트리의 특성을 반드시 유지해야하기 때문이다. 노드의 삭제는 다음의 3가지 경우를 고려하여야 한다.
-
Case1 : 단말 노드를 삭제하는 경우
-
Case2 : 자식이 하나인 노드를 삭제하려는 경우
-
Case3 : 두 개의 자식을 모두 갖고 있는 노드를 삭제하려는 경우
Case1 : 단말 노드의 삭제
가장 간단한 상황이다. 자식 노드가 없기 때문에 그 노드만 지우면 되기 때문이다. 그러나 트리에서 단말 노드를 없애는 것도 그렇게 간단하지는 않다.
-
오른쪽에 위치한 단말 노드를 없애려면 그 부모 노드의 오른쪽 자식 링크를 NULL로 변경해야 한다.
-
왼쪽에 위치한 단말 노드를 없애려면 그 부모 노드의 왼쪽 자식 링크를 NULL로 변경해야 한다.
즉, 어떤 노드를 삭제하기 위해서는 기본적으로 부모 노드도 알아야 한다. 실제로 변경되는 것도 부모의 링크 필드이다. 또한 삭제할 노드를 동적 해제하는 마무리 과정도 필요하다.
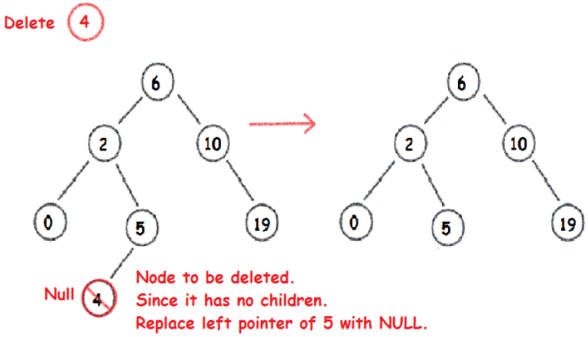
위 그림을 보면 4 노드를 삭제하려고 한다. 부모 노드의 왼쪽에 위치하고 있으므로 부모 노드 5의 왼쪽 링크를 NULL로 바꾸고 4 노드를 동적할당 해제한다.
Case2 : 자식이 하나인 노드의 삭제
이 경우도 그렇게 복잡하지 않다. 삭제할 노드의 자식이 하나뿐이면 자신을 삭제하고 유일한 자식을 부모 노드에 연결해주면 된다. 이 경우 다음을 고려해야 한다.
-
삭제할 노드의 자식이 왼쪽 자식일 수도 있고 오른쪽 자식일 수도 있다.
-
삭제할 노드가 부모의 왼쪽 자식일 수도 있고 오른쪽 자식일 수도 있다.

위 그림을 보면 10 노드를 삭제하려고 한다. 10 노드의 자식 노드 19를 부모 노드 6과 오른쪽 링크로 연결시켜주고 10 노드를 동적할당 해제한다.
Case3 : 두 개의 자식을 모두 갖는 노드의 삭제
가장 복잡한 경우이다. 어떤 두 개의 자식을 가지는 노드를 지우고 그 밑의 자식 노드를 끌어 오는 경우 자식 노드가 3개가 되는 경우가 있을 수 있다. 이는 더이상 이진트리가 아니다. 이 상황을 처리하기 위한 기본적인 아이디어는 다음과 같다.
-
먼저 삭제할 노드를 대신할 적절한 후계자 노드를 찾는다. 후계자 노드는 삭제할 노드의 왼쪽 서브트리의 가장 오른쪽에 위치하거나, 오른쪽 서브트리의 가장 왼쪽에 위치한다.
-
노드를 삭제하는 대신에 후계자 노드를 삭제위치로 복사한다. 이것은 링크가 아닌 데이터만 복사하는 것을 말한다.
-
마지막으로 후계자로 사용한 노드를 삭제한다.
후계자 노드는 지울 노드에 왼쪽 서브트리에서 가장 큰값, 혹은 오른쪽 서브트리에서 가장 작은 값이 된다. 중위 순회를 했을때 이 두 값들은 지울 노드 바로 전후에 위치한다. 그렇기 때문에 지울 노드의 키값을 대체하는데에 적합한 후계자 노드라고 할 수 있다.
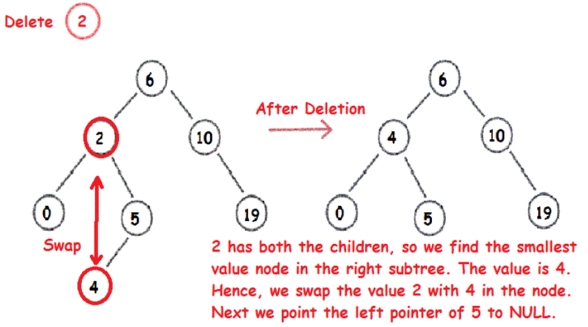
위 그림을 보면 2 노드를 지우려고 한다. 2 노드를 대체할 후계자 노드를 찾는다. 오른쪽 서브트리의 가장 왼쪽에 위치한 가장 작은 값인 4 노드가 가장 적합한 후계자 노드이다. 4 노드의 데이터를 2 노드에 복사한다. 그리고 후계자 노드는 동적할당 해제된다.
후계자 노드는 어떻게 찾을까? 삭제되는 노드의 오른쪽 서브트리에서 가장 작은 값을 갖는 노드는 오른쪽 서브 트리에서 왼쪽 링크를 타고 NULL를 만날 때까지 계속 진행하면 된다.
하지만 상황에 따라 삭제를 위해 필요한 정보가 더 있을 수 있기 때문에 구현은 훨씬 복잡해진다. 어떤 경우가 있는지 살펴보겠다.
-
삭제할 노드의 오른쪽 서브트리의 후계자 노드가 오른쪽 자식 노드를 가지고 있는 경우
-
삭제할 노드의 왼쪽 서브트리의 후계자 노드가 왼쪽 자식 노드를 가지고 있는 경우
그림으로 표현하면 다음과 같은 상황이다.
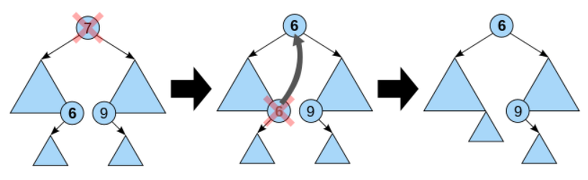
이 경우는 후계자 노드의 자식노드를 후계자 노드로 대신하면 된다. 후계자 노드를 동적할당 해제 하고 그 자리를 자식 노드에 데이터와 링크를 복사해주면 된다.
코드로 표현하면 다음과 같다.
void Delete(NODE* p, NODE* n)
{
// n은 삭제할 노드
// p는 삭제할 노드의 부모노드
// case 1 : 단말노드인 경우
if (nullptr == n->left && nullptr == n->right)
{
// 만약 루트 노드라면 루트 노드를 삭제한다.
if (nullptr == p)
m_Root = nullptr;
else
{
// 부모에서 삭제할 노드의 링크를 끊는다.
if (n == p->left)
p->left = nullptr;
else
p->right = nullptr;
}
}
// case 2 : 자식이 하나인 노드의 경우
else if (nullptr == n->left || nullptr == n->right)
{
// 삭제할 노드의 자식이 있는 곳의 노드를 받아온다.
NODE* child = (nullptr != n->left) ? n->left : n->right;
// 지울 노드가 루트 노드라면 child로 루트노드를 대신한다.
if (m_Root == n)
m_Root = child;
else
{
// 삭제할 노드가 부모의 왼쪽 자식 노드라면 왼쪽 자식 노드를 child로 대신한다.
// 혹은 오른쪽 자식 노드라면 오른쪽 자식 노드를 child로 대신한다.
if (n == p->left)
p->left = child;
else
p->right = child;
}
}
// case 3 : 자식이 둘인 노드의 경우
else
{
// 후계자 노드의 부모노드 childParent
// 후계자 노드 child
NODE* childParent= n;
NODE* child = n->right;
// 최적의 후계자 노드를 찾기 위해
// 오른쪽 서브트리의 가장 왼쪽 노드를 찾는다.
while (nullptr != child->left)
{
childParent = child;
child = child->left;
}
// 후계자 노드의 부모 노드의 왼쪽에 위치한다면
// 그 위치에 후계자 노드의 오른쪽 노드를 대신한다.
// 오른쪽에 위치한다면 그곳을 대신한다.
if (child == childParent->left)
childParent->left = child->right;
else
childParent->right = child->right;
// 지울 노드 위치의 데이터를 후계자 노드의 데이터로 복사한다.
n->data = child->data;
// 대체가 완료되었으므로 이제 불필요한 후계자 노드를 지운다.
n = child;
}
// 지울 노드를 동적할당 해제한다.
SAFE_DELETE(n);
}
이진탐색트리의 구현
이제 위 알고리즘 들을 바탕으로 이진탐색트리를 코드로 구현해보도록 하겠다. 앞서 봤던 이진트리의 연산들에 대한 설명은 생략하겠다.
미리 컴파일하는 헤더
// pch.h
#ifndef PCH_H
#define PCH_H
// 여기에 미리 컴파일하려는 헤더 추가
#include <iostream>
#include <queue>
using namespace std;
#include "DataType.h"
#include "Macro.h"
#endif //PCH_HDataType.h
#pragma once
typedef int DATA;
typedef struct _Node
{
DATA data;
_Node* left;
_Node* right;
}NODE;데이터는 키값을 저장하며 나머지는 이진트리구현때 봤던 내용과 동일하다.
Macro.h
#pragma once
template<typename T>
inline void SAFE_DELETE(T& value)
{
if (nullptr != value)
{
delete value;
value = nullptr;
}
}안전한 동적할당 해제를 위한 인라인 템플릿 함수를 선언하였다.
BinarySearchTree 클래스
앞에서 봤던 삽입, 검색, 삭제 외에 사용의 편의성을 위해 3가지 함수를 추가하였다.
-
Search_BST(int key) : key를 전달하면 전체 트리에서 해당 노드를 찾는다. 이때 Search()연산을 사용한다. 탐색이 성공한 경우와 실패한 경우에 대해 각각 화면으로 출력한다.
-
Insert_BST(int key) : key를 가진 노드를 생성하고 이진탐색트리에 삽입한다. 이 함수에서 Insert()연산을 사용한다. 화면 출력은 없다.
-
Delete_BST(int key) : key를 전달 노드를 전체 트리에서 찾아 삭제한다. 이 함수에서 Delete()연산을 사용한다. 삭제할 노드가 없는 경우 화면으로 메시지를 출력한다.
// BinarySearchTree.h
#pragma once
class BinarySearchTree
{
public:
BinarySearchTree();
~BinarySearchTree();
public:
bool IsEmpty() { return (nullptr == m_Root); }
NODE* GetRoot() { return m_Root; }
public:
void InOrder(NODE* root);
void PreOrder(NODE* root);
void PostOrder(NODE* root);
void LevelOrder(NODE* root);
public:
int CountNode(NODE* root);
int CountLeaf(NODE* root);
int CalcHeight(NODE* root);
public:
NODE* Search(NODE* n, int key);
void Search_BST(int key);
bool Insert(NODE* r, NODE* n);
void Insert_BST(int key);
void Delete(NODE* p, NODE* n);
void Delete_BST(int key);
private:
void ClearAll(NODE* root);
private:
NODE* m_Root = nullptr;
};
// BinarySearchTree.cpp
#include "pch.h"
#include "BinarySearchTree.h"
BinarySearchTree::BinarySearchTree()
{
}
BinarySearchTree::~BinarySearchTree()
{
ClearAll(m_Root);
}
void BinarySearchTree::InOrder(NODE* root)
{
if (nullptr == root)
return;
// 중위 순회
InOrder(root->left);
cout << "[" << root->data << "] ";
InOrder(root->right);
}
void BinarySearchTree::PreOrder(NODE* root)
{
if (nullptr == root)
return;
// 전위 순회
cout << "[" << root->data << "] ";
PreOrder(root->left);
PreOrder(root->right);
}
void BinarySearchTree::PostOrder(NODE* root)
{
if (nullptr == root)
return;
// 후위 순회
PostOrder(root->left);
PostOrder(root->right);
cout << "[" << root->data << "] ";
}
void BinarySearchTree::LevelOrder(NODE* root)
{
if (nullptr == root)
return;
// 큐를 이용한 레벨 순회
queue<NODE*> q;
q.push(root);
while (!q.empty())
{
NODE* node = q.front();
if (nullptr != node)
{
cout << "[" << node->data << "] ";
q.push(node->left);
q.push(node->right);
}
q.pop();
}
}
int BinarySearchTree::CountNode(NODE* root)
{
// 노드의 갯수
if (nullptr == root)
return 0;
return 1 + CountNode(root->left) + CountNode(root->right);
}
int BinarySearchTree::CountLeaf(NODE* root)
{
// 리프노드의 갯수
if (nullptr == root)
return 0;
if (nullptr == root->left && nullptr == root->right)
return 1;
else
return CountLeaf(root->left) + CountLeaf(root->right);
}
int BinarySearchTree::CalcHeight(NODE* root)
{
// 높이 구하기
if (nullptr == root)
return 0;
return 1 + max(CalcHeight(root->left), CalcHeight(root->right));
}
NODE* BinarySearchTree::Search(NODE* n, int key)
{
if (nullptr == n) // 노드에 동일한 키가 없으므로 탐색에 실패
return nullptr;
else if (n->data == key) // 노드에 키와 동일하다면 값을 찾은것
return n;
else if (n->data > key)
return Search(n->left, key); // 키가 노드보다 작은경우 왼쪽서브트리에서 찾는다.
else
return Search(n->right, key); // 키가 노드보다 큰경우 오른쪽서브트리에서 찾는다.
}
void BinarySearchTree::Search_BST(int key)
{
NODE* n = Search(m_Root, key);
if (nullptr != n)
cout << "[탐색 연산] : 성공, " << "[" << n->data << "] = "
<< std::hex << n << endl;
else
cout << "[탐색 연산] : 실패, No " << key << endl;
cout << std::dec;
}
bool BinarySearchTree::Insert(NODE* r, NODE* n)
{
if (n->data == r->data)
return false; // 이미 동일한 키가 존재하므로 삽입불가능(탐색 성공)
else if (n->data < r->data)
{
if (nullptr == r->left)
r->left = n; // 탐색에 실패한 위치에 새로운 노드 삽입
else
Insert(r->left, n); // 아직 찾아야 할 서브트리가 남아있음
}
else
{
if (nullptr == r->right)
r->right = n; // 탐색에 실패한 위치에 새로운 노드 삽입
else
Insert(r->right, n); // 아직 찾아야 할 서브트리가 남아있음
}
return true;
}
void BinarySearchTree::Insert_BST(int key)
{
NODE* n = new NODE;
n->data = key;
n->left = nullptr; n->right = nullptr;
if (IsEmpty())
m_Root = n;
else if (!Insert(m_Root, n))
SAFE_DELETE(n);
}
void BinarySearchTree::Delete(NODE* p, NODE* n)
{
// n은 삭제할 노드
// p는 삭제할 노드의 부모노드
// case 1 : 단말노드인 경우
if (nullptr == n->left && nullptr == n->right)
{
// 만약 루트 노드라면 루트 노드를 삭제한다.
if (nullptr == p)
{
SAFE_DELETE(m_Root);
}
else
{
// 부모에서 삭제할 노드의 링크를 끊는다.
if (n == p->left)
p->left = nullptr;
else
p->right = nullptr;
}
}
// case 2 : 자식이 하나인 노드의 경우
else if (nullptr == n->left || nullptr == n->right)
{
// 삭제할 노드의 자식이 있는 곳의 노드를 받아온다.
NODE* child = (nullptr != n->left) ? n->left : n->right;
// 지울 노드가 루트 노드라면 child로 루트노드를 대신한다.
if (m_Root == n)
m_Root = child;
else
{
// 삭제할 노드가 부모의 왼쪽 자식 노드라면 왼쪽 자식 노드를 child로 대신한다.
// 혹은 오른쪽 자식 노드라면 오른쪽 자식 노드를 child로 대신한다.
if (n == p->left)
p->left = child;
else
p->right = child;
}
}
// case 3 : 자식이 둘인 노드의 경우
else
{
// 후계자 노드의 부모노드 childParent
// 후계자 노드 child
NODE* childParent = n;
NODE* child = n->right;
// 최적의 후계자 노드를 찾기 위해
// 오른쪽 서브트리의 가장 왼쪽 노드를 찾는다.
while (nullptr != child->left)
{
childParent = child;
child = child->left;
}
// 후계자 노드의 부모 노드의 왼쪽에 위치한다면
// 그 위치에 후계자 노드의 오른쪽 노드를 대신한다.
// 오른쪽에 위치한다면 그곳을 대신한다.
if (child == childParent->left)
childParent->left = child->right;
else
childParent->right = child->right;
// 지울 노드 위치의 데이터를 후계자 노드의 데이터로 복사한다.
n->data = child->data;
// 대체가 완료되었으므로 이제 불필요한 후계자 노드를 지운다.
n = child;
}
// 지울 노드를 동적할당 해제한다.
SAFE_DELETE(n);
}
void BinarySearchTree::Delete_BST(int key)
{
NODE* parent = nullptr;
NODE* node = m_Root;
if (nullptr == node)
return;
while (nullptr != node && key != node->data)
{
parent = node;
node = (key < node->data) ? node->left : node->right;
}
if (nullptr == node)
{
cout << "Error : key is not in the tree!\n";
}
else
Delete(parent, node);
}
void BinarySearchTree::ClearAll(NODE* root)
{
// 모두 삭제
// 후위순회 순으로 삭제한다
if (nullptr == root)
return;
ClearAll(root->left);
ClearAll(root->right);
SAFE_DELETE(root);
}
main()
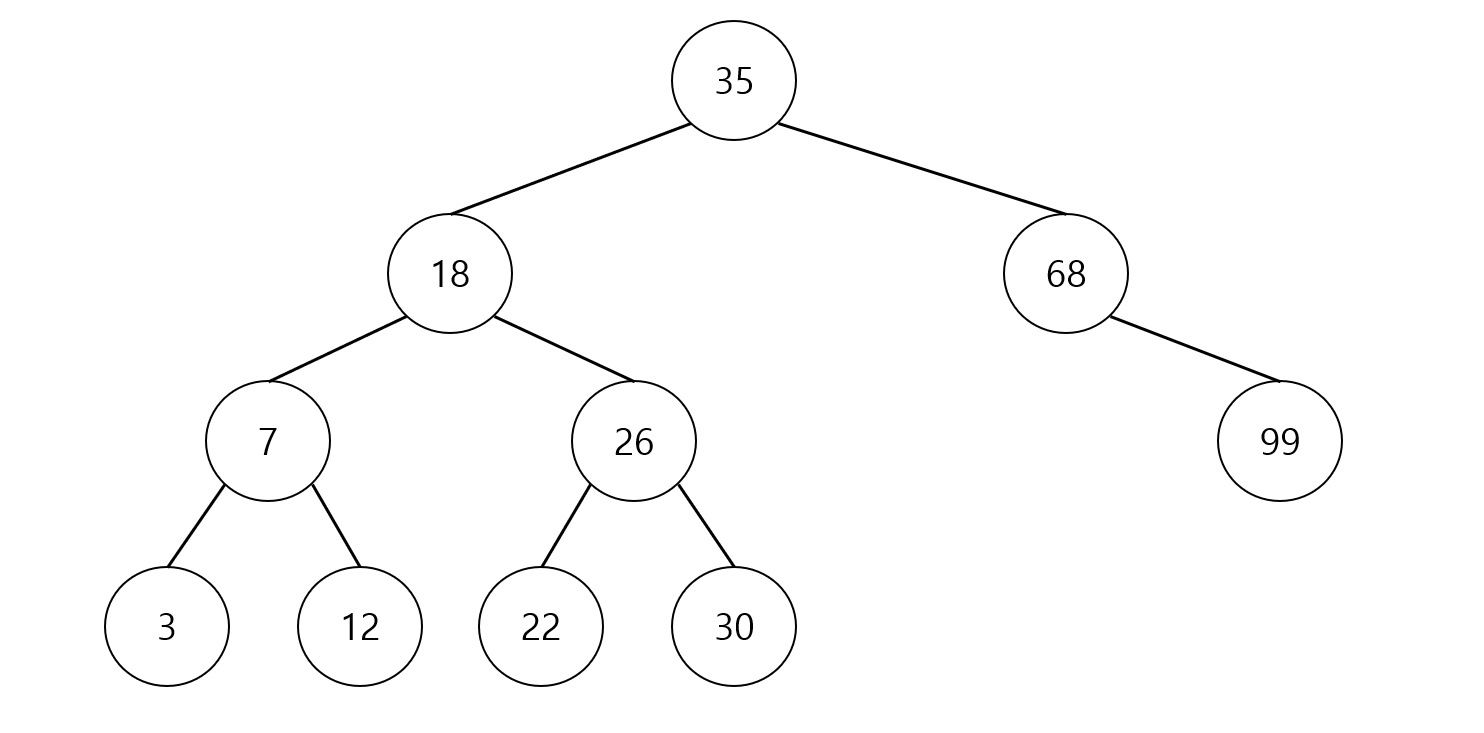
아래 그림과 같은 구조의 트리를 만들 것이다. 그리고 순회와 기타 연산으로 결과를 출력하고, 검색결과와 삭제후의 트리를 레벨 순회로 차례대로 보여준다.
#include "pch.h"
#include "BinarySearchTree.h"
int main()
{
BinarySearchTree tree;
cout << "[삽입 연산] : 35 18 7 26 12 3 68 22 30 99";
tree.Insert_BST(35); tree.Insert_BST(18);
tree.Insert_BST(7); tree.Insert_BST(26);
tree.Insert_BST(12); tree.Insert_BST(3);
tree.Insert_BST(68); tree.Insert_BST(22);
tree.Insert_BST(30); tree.Insert_BST(99);
// 트리 정보 출력
cout << "\n In-Order : "; tree.InOrder(tree.GetRoot());
cout << "\n Pre-Order : "; tree.PreOrder(tree.GetRoot());
cout << "\n Post-Order : "; tree.PostOrder(tree.GetRoot());
cout << "\nLevel-Order : "; tree.LevelOrder(tree.GetRoot());
cout << "\n 노드의 개수 = " << tree.CountNode(tree.GetRoot());
cout << "\n 단말의 개수 = " << tree.CountLeaf(tree.GetRoot());
cout << "\n 트리의 높이 = " << tree.CalcHeight(tree.GetRoot()) << endl;
tree.Search_BST(26);
tree.Search_BST(25);
cout << "\n Original BinTree : LevelOrder -> "; tree.LevelOrder(tree.GetRoot());
tree.Delete_BST(3);
cout << "\n Case1 : <3> 삭제, LevelOrder -> "; tree.LevelOrder(tree.GetRoot());
tree.Delete_BST(68);
cout << "\n Case2 : <68> 삭제, LevelOrder -> "; tree.LevelOrder(tree.GetRoot());
tree.Delete_BST(18);
cout << "\n Case3 : <18> 삭제, LevelOrder -> "; tree.LevelOrder(tree.GetRoot());
tree.Delete_BST(35);
cout << "\n Case3 : <35> 삭제, LevelOrder -> "; tree.LevelOrder(tree.GetRoot());
cout << "\n 노드의 개수 = " << tree.CountNode(tree.GetRoot());
cout << "\n 단말의 개수 = " << tree.CountLeaf(tree.GetRoot());
cout << "\n 트리의 높이 = " << tree.CalcHeight(tree.GetRoot()) << endl;
}
출력 값

'Data Structure' 카테고리의 다른 글
| 우선순위 큐 (Priority Queue) (0) | 2020.03.31 |
|---|---|
| 재귀 (Recursion) (0) | 2020.02.29 |
| 트리 (Tree) (0) | 2020.02.25 |
| AVL 트리 (AVL tree) (0) | 2020.02.21 |
| 큐(Queue) (0) | 2020.02.16 |




