| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 컨디션 변수
- 디자인패턴
- 그리디 알고리즘
- 그리디알고리즘
- 렌더링 파이프라인
- I/O장치
- 스케줄링
- 멀티프로세서
- directx
- 멀티쓰레드
- 병행성
- 쓰레드
- 운영체제
- Direct12
- 프로그래머스
- 다이나믹프로그래밍
- 동적계획법
- 알고리즘
- 락
- 타입 객체
- 자료구조
- 파일시스템 구현
- 백준
- 병행성 관련 오류
- OS
- 영속성
- DirectX12
- codility
- DirectX 12
- 다이나믹 프로그래밍
- Today
- Total
기록공간
2-13장. 페이징 : 더 작은 테이블 본문
페이징의 또 다른 문제점은 페이지 테이블의 크기이다. 페이지 테이블이 크면 많은 메모리 공간을 차지한다. 이전에 배열 형태를 가지는 선형 페이지 테이블(linear page table)을 예로 들어 페이지 테이블이 얼마나 많은 메모리 공간을 차지하는지 살펴보았다. (페이지 테이블이 100개 존재한다고 가정하면 무려 400MB의 메모리가 필요했었다!) 이러한 메모리 부담을 해결할 수 있는 기술을 모색해 보자.
간단한 해법 : 더 큰 페이지
페이지 테이블 크기를 간단하게 줄일 수 있는 방법이 한 가지 존재한다. 페이지 크기를 증가시키면 된다. 32비트 주소 공간에서, 이번에는 16KB 페이지를 가정해 보자. 이제는 18비트의 VPN과 14비트의 오프셋을 갖게 된다. 각 PTE의 크기(4KB)가 모두 동일하다면, 페이지 테이블에 2^18개의 항목이 있으며, 페이지 테이블의 총 크기는 1MB이다. 기존 페이지 테이블 대비 크기가 1/4로 감소하였다.
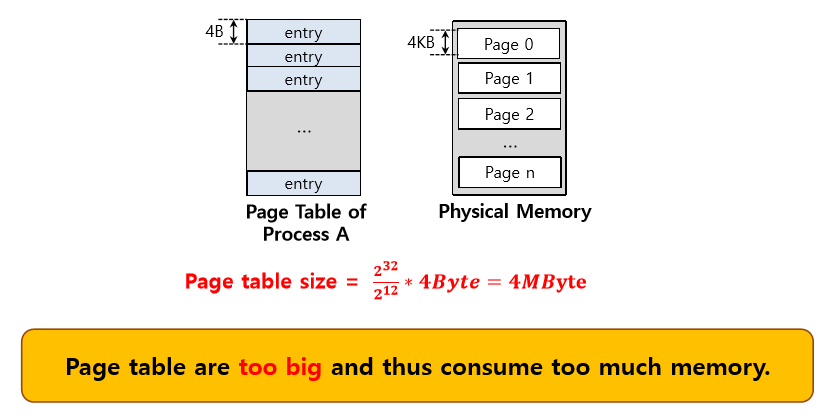

하지만 페이지 크기 증가는 부작용을 수반한다. 가장 큰 문제는 페이지 내부의 낭비 공간이 증가하는 것이다. 이를 내부 단편화(Internal fragmentation)이라고 한다.(페이지 내부에서 낭비가 발생하기 때문) 응용 프로그램이 여러 페이지를 할당받았지만, 할당받은 페이지의 일부분만 사용하는 터에, 결국 컴퓨터 시스템의 메모리가 금방 고갈되는 현상이 발생한다. 이런 이유로, 많은 컴퓨터 시스템들이 비교적 작은 페이지들을 사용한다. 크기 문제는 단순히 이런 식으로 간단히 해결할 문제가 아니다.

하이브리드 접근 방법 : 페이징과 세그멘트
인생의 어떤 일을 함에 있어 가장 좋은 방법이 두 가지 있다면, 그 두 방법을 잘 조합하여, 장점만을 취할 수는 없는지도 검토해 보아야 한다. 두 가지 방법을 조합하는 것을 하이브리드(Hybrid)라고 부른다.
Multics의 창시자 Jack Dennis는 페이징과 세그멘테이션을 결합하여 페이지 테이블 크기를 줄이는 아이디어를 내었따. 선형 페이지 테이블의 동작을 면밀히 분석해 보면, 페이징과 세그멘테이션을 효과적으로 결합할 수 있다는 사실을 발견할 수 있다.
세그멘테이션에서는 세그멘트의 물리 주소 시작 위치를 나타내는 베이스 레지스터, 그리고 크기를 나타내는 바운드 레지스터가 있다. 여기서 베이스 레지스터는 세그멘트의 시작 주소를 가리키는 것이 아니라 세그멘트의 페이지 테이블의 시작 주소를 갖는다. 그리고 바운드 레지스터는 페이지 테이블의 끝을 나타내기 위해서 사용한다.
간단한 예를 들어보자. 4KB 페이지를 갖는 32비트 가상 주소 공간이 4개의 세그멘트로 나뉘어 있다고 가정하자. (여기서는 힙, 스택, 코드 3가지의 세그멘트를 사용하겠다)
소속 세그멘트를 나타내기 위해 상위 두 비트를 사용한다. 미사용 세그멘트는 00으로, 01은 코드를 그리고 10은 힙, 스택인 11을 나타낸다고 가정하자. 가장 주소는 다음과 같이 표현될 수 있다.

실행 중인 프로세스에서, 각 세그멘트의 베이스 레지스터는 각 세그멘트 페이지 테이블의 시작 물리 주소를 갖게 된다. 이 시스템에서 모든 프로세스들은 세 개의 페이지 테이블을 갖는다. 문맥 교환 시, 이 레지스터들은 새로 실행되는 프로세스의 페이지 테이블의 위치값으로 변경된다.
TLB 미스가 발생하면, 하드웨어는 세그멘트 비트(SN)를 사용하여 어떤 베이스와 바운드 쌍을 사용할지 결정한다. 하드웨어는 그 레지스터에 들어 있는 물리 주소를 VPN과 다음과 같은 형식으로 조작하여 페이지 테이블 항목(PTE)의 주소를 얻는다.

앞에서 살펴보았던 선형 페이지 테이블의 작동과 거의 동일하다. 유일한 차이가 있다면 하나의 페이지 테이블 베이스 레지스터를 사용하는 대신 세 개 중의 하나의 세그멘트 베이스 레지스터를 사용하는 것이다.
하이브리드 기법에서 핵심은 세그멘트마다 바운드 레지스터가 따로 존재한다는 것이다. 각 바운드 레지스터의 값은 세그멘트의 최대 유효 페이지의 개수를 나타낸다. 예를 들어, 첫 세 개의 페이지들(0, 1, 2)을 코드 세그멘트로서 사용 중이라면, 코드 세그멘트 페이지 테이블은 세 개의 항목만 할당을 받을 수 있을 것이고 바운드 레지스터는 3으로 설정된다. 해당 세그멘트의 범위가 넘어가는 곳에 대한 메모리 접근은 예외를 발생시키고, 해당 프로세스는 종료될 것이다.
이와 같은 방식으로, 하이브리드 기법은 선형 페이지 테이블에 비해 메모리 사용을 개선 시킬 수 있다. 스택과 힙 사이의 할당되지 않은 페이지들은 더 이상 유효하지 않다는 것을 표시하기 위해 페이지 테이블 상에서 더 이상 공간을 차지하지 않는다.
하지만, 이 기법 역시 문제가 없는 것은 아니다. 첫째, 여전히 세그멘테이션을 사용한다. 이 전에 언급했듯이, 세그멘테이션은 주소 공간의 사용에 있어 특정 패턴을 가정하기 때문에 우리가 원하는 만큼은 유연하지가 못하다. 큰 공간을 커버하지만, 드문드문 사용되는 힙의 경우에는 여전히 페이지 테이블의 낭비를 면치 못할 수가 있다. 둘째, 하이브리드 기법은 외부 단편화를 유발한다. 하이브리드 방식에서는 페이지 테이블 크기에 제한이 없으며 다양한 크기를 갖는다. 때문에, 메모리상에서 페이지 테이블용 공간을 확보하는 것이 더 복잡하다.
멀티 레벨 페이지 테이블
어떻게 하면 사용하지 않는 주소 공간을 페이지 테이블에서 제거할 수 있을까? 이번에 소개할 기법은 멀티 레벨 페이지 테이블이다. 멀티 레벨 페이지 테이블에서는 선형 페이지 테이블을 트리 구조로 표현한다. 매우 효율적이기 때문에 많은 현대 시스템에서 사용되고 있다.
멀티 레벨 페이지 테이블의 기본 개념은 간단하다. 먼저, 페이지 테이블을 페이지 크기의 단위로 나눈다. 그 다음, 페이지 테이블의 페이지가 유효하지 않은 항목만 있으면, 해당 페이지를 할당하지 않는다. 페이지 디렉터리(Page directory) 라는 자료 구조를 사용하여 페이지 테이블 각 페이지의 할당 여부와 위치를 파악한다. 페이지 디렉터리는 페이지 테이블을 구성하는 각 페이지의 존재 여부와 위치 정보를 가지고 있다.

위 그림 예제를 한번 보자. 좌측 그림은 전형적인 선형 페이지 테이블이다. 페이지 테이블의 중앙부에 해당하는 주소 공간은 사용되고 있지 않다. 우측은 동일한 주소 공간을 다루는 멀티 레벨 페이지 테이블이다. 페이지 디렉터리에는 두 개의 유효한 페이지가 있다.(첫번째와 마지막)
이 예를 통해 멀티 레벨 페이지 테이블의 동작을 좀 더 쉽게 알 수 있다. 선형 페이지 테이블에서 사용되었던 페이지들이 더 이상 필요없고, 페이지 디렉터리를 이용하여 페이지 테이블의 어떤 페이지들이 할당되었는지를 관리한다.
페이지 데렉터리의 각 항목은 페이지 테이블의 한 페이지를 나타낸다. 페이지 디렉터리는 페이지 디렉터리 항목(Page Directory Entries, PDE)들로 구성된다. 각 항목의 구성은 페이지 테이블의 각 항목(PTE)과 유사하다. 유효(Valid) 비트와 페이지 프레임 번호(PFN) 를 갖고 있다. 실제 구현에 따라 추가 구성 요소가 존재할 수 있다.
하지만 PTE의 유효 비트와 PDE의 유효 비트는 약간 다르다. PDE 항목이 유효하다는 것은, 페이지들 중 최소한 하나가 유효하다는 것을 의미한다. 즉, PDE가 가리키고 있는 페이지 내의 최소한 하나의 PTE의 valid bit가 1로 설정되어 있다. 만약 PDE의 항목이 할당되어 있지 않다면, PDE는 실제 페이지가 할당되어 있지 않은 것이다.
멀티 레벨 페이지 테이블은 몇가지 장점이 있다. 첫째, 멀티 레벨 페이지 테이블은 사용된 주소 공간의 크기의 비례하여 페이지 테이블 공간이 할당된다. 그렇기 때문에, 보다 작은 크기의 페이지 테이블로 주소 공간을 표현할 수 있다.
두 번째, 페이지 테이블을 페이지 크기로 분할함으로써 메모리 관리가 매우 용이하다. 페이지 테이블을 할당하거나 확장할 때, 운영체제는 free 페이지 풀에 있는 빈 페이지를 가져다 쓰면 된다. 선형 페이지 테이블 방식과 다르게 연속된 메모리를 요구하지 않는다. 그렇기 때문에 추가, 삭제가 편하다.
멀티 레벨 페이지 테이블은 단점도 몇 가지 존재한다. 첫째, 멀티 레벨 테이블에는 추가 비용이 발생한다. TLB 미스 시, 주소 변환을 위해 두 번의 메모리 로드가 발생한다.(페이지 디렉터리, PTE 접근) 선형 페이지 테이블은 한 번의 접근만으로 주소 정보를 TLB에 탑재한다. 멀티 레벨 테이블은 시간과 공간을 상호 절충(time-space-trade-offs)한 예라 할 수 있다. 페이지 테이블 크기를 줄이는 데 성공하였으나, 대신 메모리 접근 시간이 증가하였다.
두 번째 단점은 복잡도이다. 페이지 테이블 검색이 선형 페이지 테이블의 경우보다 더 복잡해진다. 대부분의 경우, 성능 개선이나 부하 경감을 위해, 보다 복잡한 기법을 도입하기 마련이다. 멀티 레벨 페이지 테이블의 경우에는 메모리 자원의 절약을 위해, 페이지 테이블 검색을 좀 더 복잡하게 만들었다.
멀티 레벨 페이징 예
앞서 살펴본 개념 이해를 위해 예제를 하나 살펴보자. 64비트 페이지를 갖는 16KB 크기의 작은 주소 공간을 생각해 보자. 14비트 가상 주소 공간이다. VPN에 8비트, 페이지 오프셋에 6비트가 필요하다. 선형 페이지 테이블은 2^8(256)개 엔트리로 구성된다. 주소 공간에서 작은 부분만 사용된다 하더라도, 선형 페이지 테이블의 크기는 변하지 않는다. 다음 그림은 이 구조를 갖는 주소 공간의 예시를 보여준다.

가상 페이지 0과 1은 코드, 가상 페이지 4와 5는 힙 그리고 가상 페이지 254와 255는 스택으로 사용된다. 주소 공간의 나머지 페이지들은 미사용 중이다.
이 주소 공간을 2단계 페이지 테이블로 구성해 보자. 선형 페이지 테이블을 페이지 단위로 분할한다. 전체 테이블은 총 256개의 항목을 갖고 있다는 것을 상기하자. 각 PTE는 4바이트라 가정한다. 페이지 테이블의 크기는 1KB이다. 페이지가 64바이트라고 하면 1KB의 페이지 테이블은 16개의 64바이트 페이지들로 분할된다. 각 페이지에는 16개의 PTE가 있다.
이제 VPN으로부터 페이지 디렉터리 인덱스를 추출하고, 페이지 테이블의 각 페이지 위치를 파악하는 법을 살펴보자. 페이지 데릭터리, 페이지 테이블의 페이지들 모두 항목의 배열이라는 것을 기억해야 한다. VPN을 이용하여 인덱스를 구성하는 법만 찾으면 된다.
먼저 페이지 디렉터리의 인덱스를 만들어보자. 위의 작은 페이지 테이블은 256개의 항목으로 16개의 페이지로 나뉘어 있다. 페이지 디렉터리는 페이지 테이블의 각 페이지마다 하나씩 있어야하기 때문에 총 16개의 항목이 있어야 한다. 결과적으로 VPN의 4개의 비트를 사용하여 디렉터리를 구성하며, 여기서는 VPN의 상위 4비트를 다음과 같이 사용한다.

VPN에서 페이지-디렉터리 인덱스(줄여서 PDIndex라고 하겠다)를 추출하고 나면
PDEAddr = PageDirBase + (PDIndex * sizeof(PDE)) 라는 간단한 식을 사용하여 페이지-디렉터리 항목(PDE)의 주소를 찾을 수 있다. 이렇게 페이지 디렉터리가 구성이 된다.
페이지 디렉처리의 해당 항목이 무효라고 표시되어 있으면, 이 주소 접근은 유효하지 않기 때문에 예외가 발생한다. 해당 PDE가 유효하다면 추가 작업을 해야 한다. 이 페이지 디렉터리 항목이 가리키고 있는 페이지 테이블의 페이지에서 원하는 페이지 테이블 항목(PTE)을 읽어 들이는 것이 목표다. 이 PTE를 찾기 위해서 VPN의 나머지 비트들을 사용한다.

페이지-테이블 인덱스(줄여서 PTindex라고 하겠다)는 페이지 테이블 자체 인덱스로 사용된다. PTE 주소를 다음과 같이 계산한다. PTEAddr = (PDE.PFN << SHIFT) + (PTIndex * sizeof(PTE)).
PTE의 주소를 생성하기 위해서는 페이지-디렉터리 항목에서 얻은 페이지-프레임 번호(PFN)를 먼저 좌측 쉬프트 연산하고 그 값을 페이지 테이블 인덱스에 합산한다.
마지막으로 최종 주소 변환을 해 보자. VPN의 254의 0번째 바이트를 가리키는 주소는 다음과 같다. 0x3F80 또는 이진수로 11 1111 1000 0000 이다.
페이지 디렉터리 내에서 각 항목을 가르키기 위해 VPN의 상위 4비트를 사용하였다. 1111은 페이지 디렉터리의 마지막 엔트리다. 페이지 디렉터리의 15번째 엔트리에는 물리 프레임 주소 101이 저장되어 있다. VPN의 다음과 4비트를 (1110) 인덱스로 사용하여, 페이지 테이블의 해당 페이지에서 원하는 PTE를 찾는다. 1110는 101번 페이지의 16개의 항목 중에 마지막에서 두 번째 항목이다. 여기에 55가 젖아되어 있다. 종합하면 가상 주소 페이지 254(1111 1110)는 물리 페이지 55에 존재한다. 오프셋 000000과 PFN 55를 결하하여 다음과 같이 물리 주소를 구할 수 있으며, 해당 메모리를 접근하는 데 사용된다. PhysAddr = (PTE.PFN << SHIFT) + offset = 00 1101 1100 0000 = 0x0DC0.
2단계 이상 사용하기
지금까지 멀티 레벨 페이지 테이블은 페이지 디렉터리와 페이지 테이블의 2개 단계를 가정하였다. 경우에 따라서 트리의 단계를 더 증가시키는 것도 가능하다.
예를 들어보자. 이 예에서는 512바이트 페이지와 30비트 가상 주소 공간을 가정한다. 가상 주소는 21비트의 가상 페이지 번호와 9비트의 오프셋을 갖게 된다.
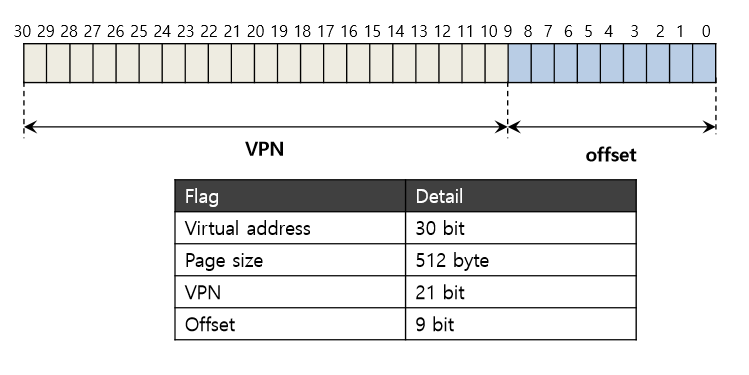
멀티 레벨 페이지 테이블의 목적은 페이지 테이블의 모든 분할된 부분들이 단일 페이지 크기에 맞도록 하는 것이다.
멀티 레벨 테이블에서 몇 단계를 둘지 정하기 위해서는 먼저 한 페이지에 몇 개의 페이지 테이블 항목을 저장할 수 있을지를 계산해야 한다. 페이지 크기가 512바이트이고 PTE의 크기가 4바이트라고 가정하면 한 페이지에 128개의 PTE를 넣을 수 있다. 페이지 테이블의 페이지를 인덱스로 쓰려면, VPN의 하위 7비트(log2(128))가 필요하다.

페이지 디렉터리를 위해 몇 개의 비트가 남았는지를 이 그림에서 알 수 있다. 14개의 비트가 남는다. 2단계 페이지를 사용한다면, 페이지 디렉터리에 2^14개의 항목이 있게 된다. 페이지 디렉터리를 위해서 128페이지 분량의 연속된 메모리가 필요하다. 페이지 테이블을 페이지 단위로 나누어 배치할 수 있도록 하는 멀티 레벨 페이지 테이블의 근본 취지가 훼손된 셈이다.

이 문제를 새결하기 위해, 페이지 디렉터리 자체를 멀티 페이지들로 나누어서 트리의 단계를 늘리도록 한다. 그리고 페이지 디렉터리의 페이지들을 가리킬 수 있도록 그 위에 새로운 페이지 디렉터리를 추가한다. 결과적으로 다음과 같이 가상 주소를 분할할 수 있다.
이제 가상 주소의 최상위 비트들을 사용하여 상위 단계의 페이지 디렉터리에서 엔트리를 찾는다. 이 인덱스를 사용하여 상위 단계 페이지 디렉터리에서 페이지 디렉터리 항목을 가져온다. 만약 유효하다면, 상위 단계 페이지 디렉터리에서 얻은 물리 주소와 두 번째 단계의 페이지 디렉터리 인덱스를 결합하여 페이지 테이블 인덱스가 존재한 물리 페이지를 구한다. 해당 페이지가 유효할 경우, 최종적으로, PTE 주소는 2번째 단계의 페이지 디렉터리 항목에서 얻은 페이지 테이블의 물리 주소와 페이지 테이블 인덱스를 결합하여 구한다. 실제 주소를 구하는 데 드는 작업이 상당하다. 멀티 레벨 페이지 테이블 사용 시 수반되는 작업이기도 하다.
'OS' 카테고리의 다른 글
| 2-15장. 물리 메모리 크기의 극복 : 정책 (0) | 2020.04.06 |
|---|---|
| 2-14장. 물리 메모리 크기의 극복 : 메커니즘 (0) | 2020.04.03 |
| 2-12장. 페이징 : 더 빠른 변환(TLB) (0) | 2020.03.21 |
| 2-11장. 페이징 : 개요 (0) | 2020.03.20 |
| 2-10장. 빈 공간 관리(메모리) (0) | 2020.03.18 |




