| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 디자인패턴
- I/O장치
- OS
- 렌더링 파이프라인
- Direct12
- 타입 객체
- 다이나믹 프로그래밍
- 다이나믹프로그래밍
- 파일시스템 구현
- 병행성
- codility
- 프로그래머스
- 영속성
- 그리디알고리즘
- 동적계획법
- 알고리즘
- 자료구조
- 병행성 관련 오류
- 컨디션 변수
- 멀티쓰레드
- 운영체제
- 스케줄링
- 쓰레드
- 락
- 멀티프로세서
- 그리디 알고리즘
- directx
- 백준
- DirectX 12
- DirectX12
- Today
- Total
기록공간
3-5장. 락 기반 병렬 자료 구조 본문
흔하게 사용되는 자료 구조에서 락을 사용하는 방법을 살펴보도록 하겠다. 자료 구조에 락을 추가하여 쓰레드가 사용할 수 있도록 만들면 그 구조는 쓰레드 사용에 안전(thread safe)하다고 할 수 있다. 물론 락인 어떤 방식으로 추가되었느냐에 따라 자료 구조의 정확성과 성능을 좌우할 것이다.
병렬 카운터
카운터는 가장 간단한 자료 구조 중 하나이다. 보편적으로 사용되는 구조이면서 인터페이스가 간단하다.
간단하지만 확장성이 없음
동기화되지 않은 카운터는 몇 줄 안되는 코드로 작성할 수 있는 평범한 자료 구조이다.
다음은 락이 없는 카운터의 코드이다.
class counter_t
{
int value;
public:
counter_t() {value = 0:}
void increment() {value++;}
void decrement() {value--;}
int get() {return value;}
};위 카운터는 간단하게 구현이 가능하지만 멀티쓰레드에서 사용이 불가능하다. 카운터 값을 증감하면서 임계 영역에 대한 데이터 경쟁 문제가 생기기 때문이다.
락을 추가한 카운터 코드는 다음과 같다.
class counter_t
{
int value;
mutex c_lock;
public:
counter_t() {value = 0:}
void increment()
{
c_lock.lock();
value++;
c_lock.unlock();
}
void decrement()
{
c_lock.lock();
value--;
c_lock.unlock();
}
int get()
{
int temp;
c_lock.lock();
temp = value;
c_lock.unlock();
return temp;
}
};get()에서는 왜 락을 걸고 있는 것일까? temp를 통해 임계 영역에 대한 값 value를 읽는 도중에 다른 쓰레드에서 값을 변경할 수 있기 때문이다.
하지만 락을 추가하면서 성능에 문제가 생기게 된다. 하나의 카운터를 여러 개의 쓰레드에서 증가시키는 벤치마킹을 하면 다음 그래프와 같다. (한 쓰레드당 100만 번씩)
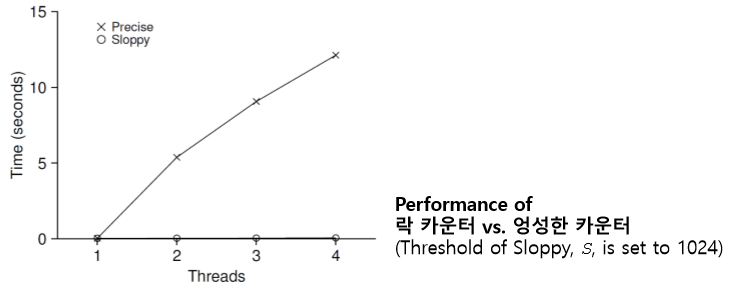
동그라미가 락이 없는 카운터, 엑스가 락이 추가된 카운터이다. 락이 추가된 카운터(동기화된 카운터)의 확장성이 많이 떨어지는 것을 볼 수 있다. 단일 쓰레드로는 카운터 값을 100만 번 갱신 갱신하는데 거의 0에 가까운 시간이 걸린다. 하지만 2개의 쓰레드로 확장하는 순간 걸리는 시간이 약 5초가 걸린다.
성능 비교
직접 벤치 마크 프로그램을 구현하여 성능을 비교해보자. 코드는 다음과 같다.
#include <thread>
#include <iostream>
#include <chrono>
using namespace std;
using namespace chrono;
class counter {...};
counter c;
void thread_func(int loops)
{
for(int i = 0; i < loops; ++i) c.increment();
}
int main()
{
thread th[8];
for(int num_th = 1; num_th <= 8; ++num_th)
{
c.reset();
// 쓰레드 수행 전 시간을 측정
auto st_t = high_resolution_clock::now();
for(int j = 0; j < num_th; ++j)
th[j] = thread{ thread_func, 10000000 / num_th };
for(int j = 0; j < num_th; ++j) th[j].join();
// 쓰레드 수행 후 시간을 측정
auto end_t = high_resolution_clock::now();
// 둘의 차를 통해 수행 시간을 구한다.
auto t = end_t - st_t;
// 수행 시간(밀리초)과 결과값을 출력한다.
cout << "Time = " << duration_cast<milliseconds>(t).count();
cout << " Result = " << c.get() << endl;
}
}
벤치마킹에 사용한 CPU는 i7 4702HQ (쿼드코어)이다.
-> 락을 사용하지 않았을 경우의 성능
class counter
{
volatile int value;
mutex c_lock;
public:
counter() {value = 0:}
void increment() {value++;}
void decrement() {value--;}
int get() {return value;}
void reset() {value = 0;}
}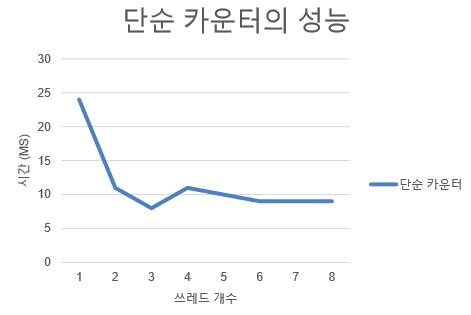
우선 확장성은 그나마 좋다고 말할 수 있다. 항상은 아니지만 쓰레드 개수가 늘어나면서 걸리는 시간이 줄어들었다. 하지만 수행 결과가 부정확하게 나왔다.
-> 락을 사용했을 경우의 성능
class counter
{
volatile int value;
mutex c_lock;
public:
counter() {value = 0:}
void increment()
{
c_lock.lock();
value++;
c_lock.unlock;
}
void decrement()
{
c_lock.lock();
value--;
c_lock.unlock();
}
int get() {return value;}
void reset() {value = 0;}
}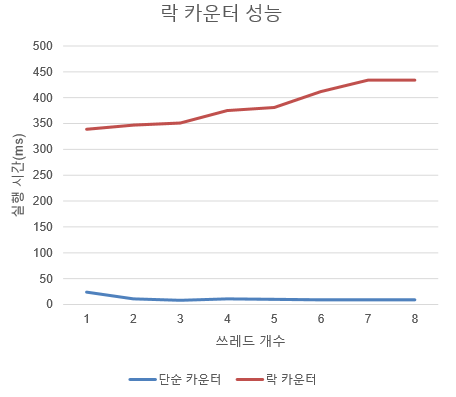
락을 추가한 카운터는 단일 쓰레드부터 벌써 성능이 안 좋으며, 쓰레드 개수가 증가할수록 더더욱 안 좋아진다. 하지만 정확한 결과값이 나오기는 한다.
결국 락 카운터는 모니터(monitor)(모든 메서드들의 실행을 자동적으로 상호 배제하는 자료구조)와 유사하며, 구현이 쉽지만 성능이 너무나도 떨어진다는 단점이 존재한다.(더 느려진다!) 병렬 자료구조는 적어도 단일 쓰레드보다 느려져서는 안 되고, 쓰레드와 CPU 개수가 늘어날수록 성능이 향상되어야 한다.
엉성한 카운터
수년 동안 확장성 있는 카운터를 만들기 위해 많은 연구가 진행되었다. 확장성 있는 카운터는 중요한 의미를 갖는다. 최근 운영체제 성능 분석 결과에 의하면, 확장 가능한 카운터가 없으면 Linux의 몇몇 작업은 멀티코어에서 심각한 확장성 문제를 겪을 수 있다고 한다.
그래서 여러 기법 중 하나를 소개한다. 바로 엉성한 카운터(sloppy counter)라고 불리는 기법이다. 이는 락카운터의 성능 개선을 위해 나온 기법으로, 락의 사용 횟수를 줄이고자 한다. (전역 변수 사용 횟수 줄이고, 쓰레드 지역 변수를 사용)
쓰레드 지역 변수(thread local strage, TLS)는 같은 전역 변수이지만, 쓰레드 마다 다른 장소에 접근이 가능하다는 특징이 있다. 가장 간단한 구현은 지역 변수를 배열로 구현해 쓰레드마다 자신의 ID로 인덱싱하는 것이다. C++11에서는 TLS 사용을 위해 thread_local 확장자를 쓴다.
엉성한 카운터의 기본 개념은 다음과 같다. 쓰레드 개수와 CPU의 개수가 같아서 각 CPU가 한 개씩의 쓰레드를 실행하기 때문에 각 CPU(or Core)는 지역 카운터를 하나씩 갖는다. 각 지역 카운터를 위한 락을 1개씩 가지고 있기 때문에 여러 개의 쓰레드를 사용하여 지역 카운터의 수정을 하여도 아무런 충돌이 없다. 그렇기 때문에 카운터 수정은 확장성이 있다.
그리고 지역 카운터 값은 주기적으로 전역 카운터에 더해진다. 이때 전역 카운터가 가지고 있는 전역 락을 얻는다. 전역 카운터에 의해 더해진 지역 카운터 값은 0으로 초기화된다.
엉성한 카운터 구현
얼마나 자주 지역에서 전역으로 전송이 필요한지 그 빈도에 대한 한계치를 s(엉성수치)로 결정한다.
다음 표는 엉성한 카운터의 흐름을 보여준다. 한계치를 5로 설정하였고 네 개의 CPU에 각 지역 카운터 L1, ..., L4를 갱신하는 쓰레드들이 있다. 전역 카운터의 값(G)도 같이 나타내었는데, 만약 지역 카운터가 한계치 s에 도달하면 지역 값은 전역 카운터에 반영되고 지역 카운터 값은 초기화된다.
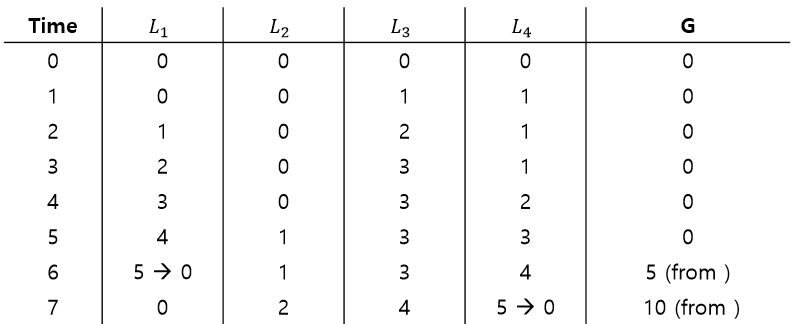
다음은 구현 코드이다. (C++11 이전 코드)
// OLD
static const int NUM_CPUS = 8;
class counter_t
{
int global; //전역 카운트
std::mutex glock; // 전역 카운트 락
int local[NUM_CPUS]; // 지역 카운트
std::mutex llock[NUM_CPUS]; // 지역 카운트 락
int threshold; // 전달 빈도수, 엉성수치 s
public:
counter_t(int threshold_v) // 생성자로 전달 빈도수를 받는다.
{
threshold = threshold_v;
global = 0;
for (int i = 0; i < NUM_CPUS; ++i) local[i] = 0;
}
void update(int threadID, int amt)
{
llock[threadID].lock();
local[threadID] += amt;
// 빈도수보다 지역 카운트가 커지면 전역 카운트에 더해주고.
// 0으로 초기화시킨다.
if (local[threadID] >= threshold)
{
glock.lock();
global += local[threadID];
glock.unlock();
local[threadID] = 0;
}
llock[threadID].unlock();
}
int get()
{
int temp;
glock.lock();
temp = global;
glock.unlock();
return temp;
}
};다음은 C++11을 이용한 구현 코드이다.
static const int NUM_CPUS = 8;
thread_local int local;
class s_counter
{
std::atomic_int global; // 아토믹 전역 변수
int threshold; // 빈도수 엉성수치 s
public:
s_counter(int threshold_v) { threshold = threshold_v; global = 0; }
void increment()
{
local++;
if (local >= threshold) { global += local; local = 0; }
}
int get() { return global; }
void flush() { global += local; local = 0; }
void reset() { global = 0; }
};
s_counter c{ 10000 };
void thread_func(int loops)
{
for (int i = 0; i < loops; ++i) c.increment();
c.flush();
}다음 그래프는 단순한 카운터와 엉성한 카운터의 성능 비교표이다. 대부분에서 단순 카운터보다 성능이 훨씬 좋았다.
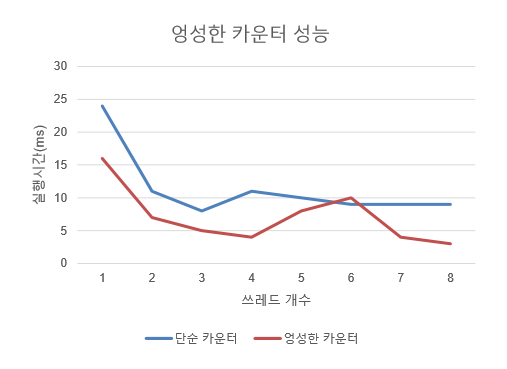
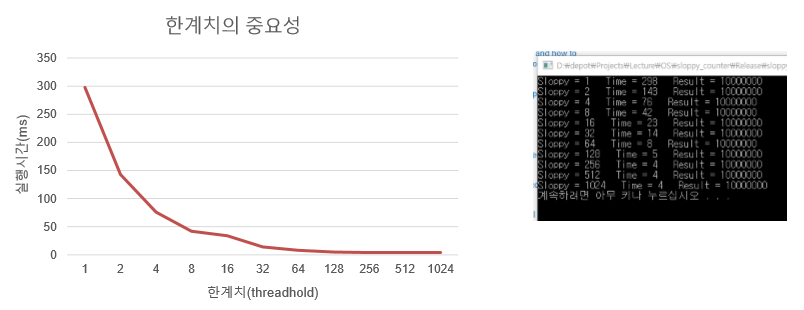
엉성한 카운터는 위에서 봤던 한계치 s가 성능과 정확성을 판가름 내리기 때문에 s가 무엇보다도 중요하다. s가 작으면 전역 카운터에 접근하는 빈도수가 높아져 낮은 성능을 보이지만, 전역 카운터는 비교적으로 정확하게 나온다. s가 크면 접근 빈도수가 낮아져 높은 성능을 보이지만, 전역 카운터가 뒤처져 정확한 값이 안 나올 수도 있다.
병렬 연결 리스트
이제 조금 더 복잡한 구조인 연결 리스트를 다룬다. 여기서는 삽입 연산만 구현한다. 나머지는 개인의 몫으로 남겨두도록 한다. 우선 코드는 다음과 같다.
class NODE
{
public:
int key = 0;
NODE* next = nullptr;
};
class LIST
{
public:
NODE* head;
std::mutex lock;
LIST() { head = nullptr; }
// 삽입
bool Insert(int key)
{
lock.lock();
NODE* p = new NODE;
if (p == nullptr)
{
// 실패
std::cout << "Can't allocate memory.";
lock.unlock(); // 교착상태를 피하기 위해 언락한다.
return false;
}
// 성공
p->key = key;
p->next = head;
head = p;
lock.unlock();
return true;
}
// 검색
bool List_Lookup(int key)
{
lock.lock();
NODE* curr = head;
while (nullptr != curr)
{
if (curr->key == key)
{
lock.unlock();
return true;
}
curr = curr->next;
}
lock.unlock();
return false;
}
};코드에서 볼 수 있듯이, 삽입 연산을 시작하기 전에 락을 획득하고 리턴 직전에 반납한다. 드물게 동적할당이 실패할 경우가 있다. 그런 경우 실패를 리턴하기 전에 쓰레드의 락을 반납하여 교착상태를 회피해야 한다. 그리고 락의 획득과 반납은 실제 임계 영역만을 둘러싸야 병행성을 늘리고 오류를 최소화할 수 있다. 아래는 이것을 반영한 수정 코드이다.
class NODE
{
public:
int key = 0;
NODE* next = nullptr;
};
class LIST
{
public:
NODE* head;
std::mutex lock;
LIST() { head = nullptr; }
// 삽입
bool Insert(int key)
{
// lock.lock();
NODE* p = new NODE;
if (p == nullptr)
{
// 실패
std::cout << "Can't allocate memory.";
lock.unlock(); // 교착상태를 피하기 위해 언락한다.
return false;
}
// 성공
p->key = key;
lock.lock(); // 이쪽으로 변경
p->next = head;
head = p;
lock.unlock();
return true;
}
// 검색
bool List_Lookup(int key)
{
bool rv = false;
lock.lock();
NODE* curr = head;
while (nullptr != curr)
{
if (curr->key == key)
{
// lock.unlock();
rv = true; // 추가
// return true;
break; // 추가
}
curr = curr->next;
}
lock.unlock();
return rv;
}
};
확장성 있는 연결 리스트
병렬 처리가 가능한 연결 리스트를 구현하였지만 이는 확장성이 좋지 않다는 문제가 있다. 그래서 병렬성을 개선하는 방법 중 하나로 hand-over-hand locking(lock coupling)이라는 기법을 개발했다.
개념은 단순하다. 전체 리스트에 하나의 락이 있는 것이 아니라 개별 노드마다 락을 추가하는 것이다. 리스트를 순회할 때 다음 노드의 락을 먼저 획득하고 지금 노드의 락을 해제하도록 한다.
개념적으로는, 리스트 연산에 병렬성이 높아지기 때문에 괜찮은 것처럼 보인다. 하지만 실제로는 락 획득과 반납 오버헤드가 매우 크기 때문에 기본 성능이 매우 낮다. 아주 큰 리스트를 굉장히 많은 수의 쓰레드가 병렬로 순회한다 해도, 락을 하나만 사용하는 것보다 빠르기 어렵다. 차라리 일정 개수의 노드를 처리할 때마다 하나의 새로운 락을 획득하는 하이브리드 방식이 더 낫다.
병렬 큐
여기서는 Michael과 Scott이 설계한 병렬성 좋은 큐에 대해 살펴본다. 이 병렬 큐는 두 개의 락이 있는데, 하나는 큐의 head에, 다른 하나는 tail에 사용된다. 이 두 개 락의 목적은 큐에 삽입(enqueue)과 추출(dequeue) 연산에 병렬성을 부여하는 것이다.
또한 더미 노드(또는 보초 노드)가 추가된다. 더미 노드는 큐가 초기화될 때 할당되며, head와 tail 연산을 서로 분리한다.
다음은 병렬 큐 코드이다.
class NODE
{
public:
int value = 0;
NODE* next = nullptr;
};
class QUEUE
{
public:
NODE* head;
NODE* tail;
std::mutex headlock, taillock;
QUEUE() { head = tail = new NODE; }
// 삽입
void Queue_Enqueue(int value)
{
NODE* tmp = new NODE;
assert(tmp != nullptr);
tmp->value = value;
tmp->next = nullptr;
// tail에 삽입을 위해 tail 락을 획득한다.
taillock.lock();
tail->next = tmp;
tail = tmp;
taillock.unlock();
}
// 검색
int Queue_Dequeue(int* value)
{
// head에서 추출을 위해 head 락을 획득한다.
headlock.lock();
NODE* tmp = head;
NODE* newHead = tmp->next;
if (newHead == nullptr)
{
headlock.unlock();
return -1; // 큐가 비어있음
}
*value = newHead->value;
head = newHead;
headlock.unlock();
delete tmp;
return 0;
}
};
병렬 해쉬 테이블
여기서는 간단한 해쉬 테이블을 구현한다. 병렬 연결 리스트를 사용하여 구현한다. 크기가 고정되어 있고, 확장이 되지 않으며, 전역 락이 없고 해시 버켓마다 락이 있다. 성능이 우수한 이유도 해시 버켓마다 락이 있기 때문이다.
간단한 해시 테이블과 확장성이 좋은 해시 테이블의 성능 그래프는 다음과 같다.
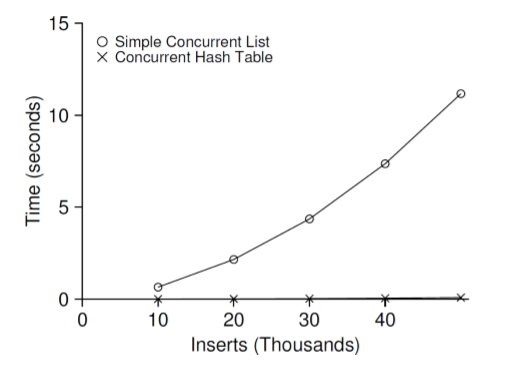
간단한 해시 테이블은 삽입 연산을 하면 할수록 시간이 기하급수적으로 증가한다는 것을 볼 수가 있다.
다음은 간단한 해시 테이블 코드이다.
#define BUCKETS (101)
class HASH_TABLE
{
LIST lists[BUCKETS];
public:
int Hash_Insert(int key)
{
int bucket = key % BUCKETS;
return lists[bucket].List_Insert(key);
}
int Hash_Lookup(int key)
{
int bucket = key % BUCKETS;
return lists[bucket].List_Lookup(key);
}
};
병렬 자료구조 그 외...
-
락 획득과 해제 시 코드의 흐름에 주의를 기울여야 한다.
- unique_lock 과 lock_guard를 사용해야 하는 이유 (이것을 사용하면 지역을 빠져나가는 경우 자동으로 락을 반납) -
임계영역의 크기를 최소화해야 한다.
- unique_lock과 lock_guard 사용 시 주의 -
병행성 개선이 반드시 성능 개선으로 이어지지는 않는다.
- 추가 오버헤드에 주의 -
미숙한 최적화(premature optomization) 주의
- 전체 성능에 미치는 영향을 계속 살펴야 한다. -
논 블럭킹 자료구조
- 성능을 위한 최선의 선택
- 하지만 구현이 너무나도 어렵다.
'OS' 카테고리의 다른 글
| 3-7장. 세마포어 (0) | 2020.05.04 |
|---|---|
| 3-6장. 컨디션 변수 (0) | 2020.05.01 |
| 3-4장. 락(Lock) - 3 (0) | 2020.04.27 |
| 3-3장. 락(Lock) - 2 (0) | 2020.04.24 |
| 3-2장. 락(Lock) - 1 (0) | 2020.04.22 |



