| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 멀티쓰레드
- 컨디션 변수
- I/O장치
- 병행성 관련 오류
- 다이나믹 프로그래밍
- 알고리즘
- Direct12
- 프로그래머스
- 운영체제
- codility
- 자료구조
- OS
- directx
- 파일시스템 구현
- 렌더링 파이프라인
- 쓰레드
- 타입 객체
- 병행성
- 백준
- 디자인패턴
- 영속성
- 그리디알고리즘
- 다이나믹프로그래밍
- DirectX 12
- 동적계획법
- 스케줄링
- 멀티프로세서
- 락
- 그리디 알고리즘
- DirectX12
- Today
- Total
기록공간
허프만(Huffman) 트리를 이용한 텍스트 압축 본문
개요
허프만 코딩(Huffman coding)은 텍스트 압축을 위해 널리 사용되는 방법으로, 원본 데이터에서 자주 출현하는 문자는 적은 비트의 코드로 변환하여 표현하고 출현 빈도가 낮은 문자는 많은 비트의 코드로 변환하여 표현함으로써 전체 데이터를 표현하는데 필요한 비트 수를 줄이는 방식이다. (마치 UTF-8과 비슷하게 동작한다)
이러한 압축 과정에서 가장 중요한 부분이 각 문자를 표현하기 위한 허프만 트리(Huffman tree)를 구성하는 것인데, 예를 통해 그 과정을 이해해 보자.
원리
다음의 텍스트를 허프만 코딩을 통해 압축해 보려고 한다.
AAAAAAABBCCCDEEEEFFFFFFG
우선 원본 데이터에 포함된 각 문자에 대한 출현 빈도수를 구하여 내림차순으로 정렬한다.
A(7개) F(6개) E(4개) C(3개) B(2개) D(1개) G(1개)
그리고 출현 빈도가 가장 작은 D와 G를 묶어 이진트리를 구성하고, 이 둘을 묶는 루트 노드에 두 문자 빈도수의 합인 2를 적는다. 이후 반도수의 합인 2를 기준으로 내림차순 재정렬이 필요한 경우 재배열한다.

마찬가지로 값이 가장 작은 두 개의 노드를 묶어 이진 트리를 구성하고, 그 루트 노드에는 두 빈도수 값의 합을 적는다. 여기서는 B와 2(D, G)가 묶이게 되며 빈도수 합은 4가 된다. 이후 합쳐진 빈도수 4를 기준으로 내림차순 재배열을 수행한다.

동일한 방법으로 다음 단계를 수행한다. 이번에는 4(B, D, G)와 C(3)이 트리로 묶이게 된다. 이때의 빈도수 합은 7이 되며, 이 값을 기준으로 내림차순 재배열을 수행한다.
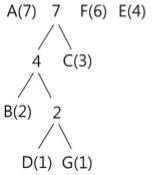
모든 노드(문자)가 트리에 포함될 때까지 이러한 과정을 반복한다. 전체 트리가 구성되는 각 단계를 차례로 나타내면 다음과 같다.

마지막으로 전체 트리에 대해 각 가지의 왼쪽에는 0, 오른쪽에는 1을 기입하여 허프만 트리를 완성시킨다. 루트로부터 가지로 숫자를 읽어 내려가면서 각 문자에 대한 이진코드를 기록한다.

이렇게 만들어진 코드를 이용해 원본 텍스트를 표현하면 아래와 같이 된다. 이는 허프만 코딩을 통해 원본 텍스트를 압축한 결과가 된다.
AAAAAAABBCCCDEEEEFFFFFFG
0000000000000001000100011011011010101111111110101010101001011
문제 해결 및 구현
이 문제는 자료구조 및 알고리즘 시간이 쉬이 접할 수 있는 개념이며 해결할 수 있는 방법이 수도 없이 많고 압축 방식 또한 다양하다. 기본적으로 가장 작은 값이 계속해서 계산에 사용된다는 점과 트리 혹은 큐 구조로 이루어진다는 것이 흥미롭게 느껴지는 알고리즘이다. 또한 계산에 있어서 '빈도수'가 기준으로 사용된다. 사실 자료구조 측면에서 보았을 때는 이미 비슷한 것들이 많이 갖추어져 있기 때문에 어렵지 않게 접근할 수 있다.
준비물 : 해시 맵, 우선순위 큐
과정
-
문자열을 입력받는다.
-
입력받은 문자열을 문자 단위로 끊어 해시 맵에 저장한 뒤 빈도수를 체크한다.
-
이후 빈도수가 1 이상인 문자에 한해 우선순위 큐에 삽입한다.
-
우선순위 큐에 삽입하면서 자동으로 빈도수라는 우선순위에 따라 최소 힙과 같은 형태가 된다.
-
루트 노드에서부터 순회하며 0 또는 1을 붙여 허프만 코딩 알고리즘을 적용한다.
-
결과적으로 처음 입력받은 문자열을 해시 맵과 대조하여 압축된 2 진수를 출력한다.
코드는 다음과 같다.
#include <iostream>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
// 노드 정보
struct Node
{
char character;
int frequency;
Node *left, *right;
};
// 우선순위 큐 정렬을 위한 구조체
// 빈도수를 기준으로 최소힙으로 정렬한다.
struct cmp
{
bool operator()(Node* A, Node* B)
{
return A->frequency > B->frequency;
}
};
class HuffmanTree
{
public:
~HuffmanTree()
{
// 동적할당 받은 노드들을 지운다.
ReleaseTree(root);
root = nullptr;
um.clear();
info.clear();
while (!pq.empty()) pq.pop();
}
public:
const unordered_map<char, string>& GetInfo()
{
// 허프만 트리로 얻은 알파벳 별 이진수 정보를 가져온다.
return info;
}
public:
// 압축할 문자열 정보를 바탕으로 허프만 트리를 만들어
// 이진수 정보들을 만든다.
void Create(const string& str)
{
// 해쉬 테이블을 이용해 빈도수를 기록
for (const auto iter : str) ++um[iter];
for (const auto iter : um)
{
// 해쉬 테이블에서 하나씩 꺼내
// 정보를 노드에 저장 후
// 우선순위 큐에 집어 넣는다.
Node* newNode = new Node;
newNode->left = nullptr;
newNode->right = nullptr;
newNode->character = iter.first;
newNode->frequency = iter.second;
pq.push(newNode);
}
// 우선순위 큐 정보를 바탕으로 트리를 만든다.
MakeTree();
// 트리를 순회하면서 이진수 정보를 입력받는다.
string tmp = "";
FindTree(root, tmp);
}
private:
void MakeTree()
{
// 우선 순위 큐를 이용해 빈도수가 작은 순으로
// 2개씩 꺼내 두 노드를 담는 노드를 만들어
// 두 노드의 빈도수를 합치고 큐에 다시 집어 넣는다.
int limit = pq.size() - 1;
for (int i = 0; i < limit; ++i)
{
Node* newNode = new Node;
newNode->character = 0;
newNode->right = pq.top(); pq.pop();
newNode->left = pq.top(); pq.pop();
newNode->frequency = newNode->right->frequency + newNode->left->frequency;
pq.push(newNode);
}
// 이 작업을 마치면 우선순위 큐에는 한가지 원소만 남는다.
// 그것이 허프만 트리의 Root 노드가 된다.
root = pq.top();
}
void FindTree(Node* p, string str)
{
if (p == nullptr) return;
// 왼쪽은 0, 오른쪽은 1
// 순회하면서 정보를 더해간다.
FindTree(p->left, str + '0');
FindTree(p->right, str + '1');
// 알파벳 정보를 가진 노드를 만날때까지 순회한다.
if (p->character != 0)
{
info[p->character] = str;
}
}
void ReleaseTree(Node* p)
{
// 후위 순화를 하면서 동적할당 했던 노드들을
// 할당 해제 시켜준다.
if (p == nullptr) return;
ReleaseTree(p->left);
ReleaseTree(p->right);
delete p;
p = nullptr;
}
private:
Node* root = nullptr;
unordered_map<char, int> um;
unordered_map<char, string> info;
priority_queue<Node*, vector<Node*>, cmp> pq;
};
int main()
{
string str = "AAAAAAABBCCCDEEEEFFFFFFG";
HuffmanTree t;
t.Create(str);
unordered_map<char, string> info = t.GetInfo();
cout << "압축할 문자열 : " << str << "\n\n";
cout << "이진수 정보 : \n";
for (const auto iter : info)
{
cout << iter.first << ": " << iter.second << endl;
}
cout << "\n압축된 정보: ";
for (const auto iter : str)
{
cout << info[iter] << ' ';
}
}
출력 값

'Algorithm > 이론' 카테고리의 다른 글
| 유클리드 알고리즘 (gcd, 최대공약수) (0) | 2020.08.22 |
|---|---|
| 구간 합(Prefix Sum) 알고리즘 (0) | 2020.07.20 |
| 다익스트라 알고리즘 (0) | 2020.07.09 |
| 백트래킹 알고리즘 (Backtracking Algorithm) (0) | 2020.06.30 |
| 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2020.06.18 |


