| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 다이나믹프로그래밍
- Direct12
- directx
- 병행성
- codility
- 병행성 관련 오류
- OS
- 자료구조
- 다이나믹 프로그래밍
- DirectX 12
- 타입 객체
- I/O장치
- 스케줄링
- 알고리즘
- 멀티쓰레드
- 파일시스템 구현
- 그리디알고리즘
- DirectX12
- 쓰레드
- 백준
- 그리디 알고리즘
- 락
- 멀티프로세서
- 운영체제
- 영속성
- 컨디션 변수
- 디자인패턴
- 프로그래머스
- 렌더링 파이프라인
- 동적계획법
- Today
- Total
기록공간
우선순위 큐 (Priority Queue) 본문
컴퓨터에서는 우선순위 개념이 종종 필요할 때가 있다. 예를 들면, 운영 시스템에서 시스템 프로세스는 응용 프로세스보다 더 높은 우선순위를 갖는다. 따라서 자료구조에서도 이러한 우선순위를 지원하는 것이 필요하다.
우선순위 큐는 이러한 우선순위의 개념을 큐에 도입한 자료구조이다. 보통의 큐는 먼저 들어온 데이터가 먼저 나가는 구조(FIFO)인데 비해, 우선 순위 큐는 모든 데이터가 우선순위를 가지고 있고, 들어온 순서와 상관없이 우선순위가 높은 데이터가 먼저 출력되는 구조다.
우선순위 큐는 사실 가장 일반적인 큐로 볼 수 있다. 이것은 우선순위 큐를 사용하여 스택이나 큐를 얼마든지 구현할 수 있기 때문이다. 예를 들어 데이터가 들어온 시점 기준으로 빠른 것을 높은 우선순위로 잡으면 큐처럼 동작하고, 반대로 늦은 것을 높은 우선순위로 잡으면 스택으로 사용할 수 있다.
우선순위 큐는 컴퓨터의 여러 분야에서 다양하게 이용된다. 시뮬레이션이나 네트워크 트래픽 제어, 운영 체제의 작업 스케줄링, 수치 해석적인 계산 등에서 활용된다. 이러한 우선순위 큐는 다른 여러 자료구조들로 구현이 가능하지만 가장 효율적인 구조는 힙(Heap)이다. 따라서 힙을 중심적으로 알아볼것이다.
힙(Heap) : 개념
힙의 뜻은 "더미" 또는 "무더기"이다. 컴퓨터 분야에서 힙은 완전이진트리 기반의 "더미"와 모습이 비슷한 특정한 자료 구조를 의미한다.

힙은 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료 구조이다. 힙은 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(또는 작은) 이전 트리를 말한다. 이진탐색트리와는 달리 힙 트리에서는 중복된 값을 허용한다.

힙은 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있는 정도의 느슨한 정렬 상태를 유지한다. 힙의 목적이 삭제 연산에서 가장 큰 값(혹은 작은 값) 을 효율적으로 찾아내기만 하면 되는 것이므로 전체를 정렬할 이유는 없다.
위 그림은 두 가지 종류의 힙 트리를 보여준다. 부모 노드의 키값이 자식 노드보다 큰 경우를 최대 힙(max heap)이라 부르고, 반대로 부모의 키 값이 자식보다 작은 것은 최소 힙(min heap)이라 부른다.

힙은 완전이진트리이다. 위 그림은 힙의 특성을 만족하는 것처럼 보이지만 완전이진트리가 아니기 때문에 힙이 아니다.

힙(Heap) : 구조
힙은 완전이진트리이기 때문에 중간에 비어있는 요소없이 차례대로 번호를 붙일 수 있다. 이 번호를 배열의 인덱스로 생각하면 배열에 힙의 노드들을 저장할 수 있다. 따라서 힙을 저장하는 효과적인 자료구조는 배열이다. 트리의 모든 위치의 노드 번호는 새로운 노드가 추가되더라도 변하지 않는다. 예를들어 루트 노드의 왼쪽 자식의 번호는 항상 2이며 오른쪽 자식은 항상 3이다.
배열을 이용하여 힙을 표현하면 자식과 부모 노드의 위치(인덱스)를 쉽게 계산할 수 있다. 어떤 노드의 왼쪽이나 오른쪽 자식의 위치는 다음과 같이 계산된다.
-
왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
-
오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
어떤 노드의 부모 인덱스를 알고 싶으면 다음과 같은 식을 사용하면 된다.
-
부모의 인덱스 = (자식의 인덱스) / 2

힙(Heap) : 연산
1. 삽입 연산
힙에 새로운 요소를 삽입하는 삽입 연산은 신입 사원이 들어오면 말단 위치에 앉힌 다음에, 능력을 봐서 위로 승진시키는 과정과 유사하다. 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드의 다음 위치에 삽입한다. 그 후 새로운 노드를, 부모 노드들과 교환해서 힙의 성질을 만족시켜 주는 과정이 필요하다. 이것을 업힙(up-heap)이라고 한다.
예를 들어 위 트리에서 8을 삽입한다고 하자. 우선 번호순으로 가장 마지막 위치에 이어서 새로운 요소 8이 삽입된다.

삽입된 요소 8이 부모 노드 4와 비교하였을때 더 크기 때문에 교환해준다.

그리고 부모 노드 7과 비교하여 삽입된 요소 8이 더 크므로 교환한다.

우선순위 큐의 삽입 절차를 의사 코드로 기술하면 다음과 같다.
insert(node)
heap_size <- heap_size + 1;
i <- heapSize;
heap[i] <- node;
// 루트노드까지 혹은 부모노드가 삽입된 요소보다 클때까지 반복
while i != 1 and KEY(heap[i]) > KEY(Parent(i)) do
// 부모노드와 삽입된 요소 위치를 바꾼다
heap[i] <-> Parent(i);
// 다음 부모 노드와 비교하기 위해 i를 i/2로 갱신한다
i <- PARENT(i);
2. 삭제 연산
힙에서 삭제 연산은 루트 노드를 삭제하는 것이다. 최대 힙에서는 루트가 최댓값을 가지므로 (최소 힙에서는 최소값) 루트 노드를 삭제하고 힙의 성질을 계속 유지하기 위해 힙 트리를 재구성해야 한다. 힙트리 재구성을 위한 기본 아이디어는 회사에서 사장의 자리가 비게 되면 먼저 제일 만단 사원을 사장 자리로 올린 다음에 순차적으로 강등시키는 것과 비슷하다. 이 과정을 다운힙(down-heap)이라 한다.
다음 힙 트리에서 루트 노드를 삭제해 보자.

루트 노드를 삭제하고 빈 루트 노드 자리에는 힙의 마지막 모드를 가져온다.

새로운 루트노드인 3과 자식 노드들을 비교해보면 자식 노드가 더 크기 때문에 교환이 일어난다. 이때, 자식 중에서 더 큰 노드와 비교하고 교환해야 함에 유의하자. 따라서 3과 7이 교환된다.
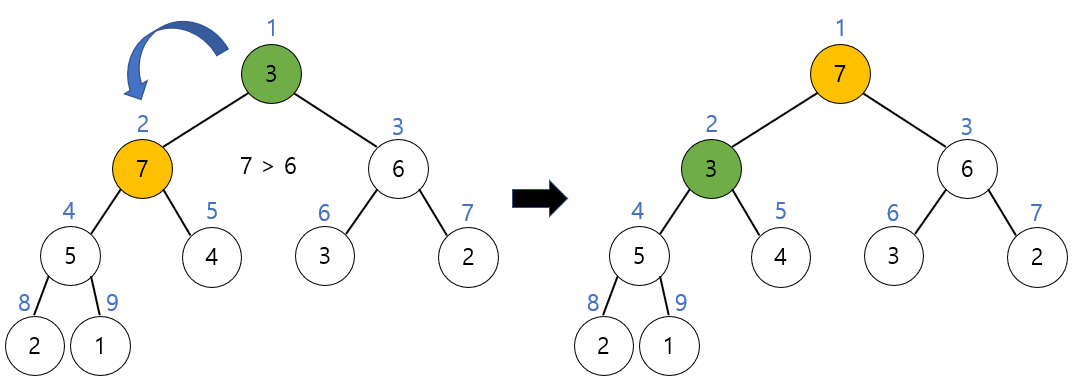
교환된 이후에도 3이 자식 노드보다 더 작기 때문에 3과 자식 노드 5를 교환한다.

3이 자식 노드인 2과 1보다 크기 때문에 더 이상의 교환은 필요 없다.
이 과정은 의사코드로 표현하면 다음과 같다.
remove()
// 삭제된 루트 노드자리에 말단 노드를 배치한다
root <- A[1];
A[1] <- A[heapSize];
heapSize <- heapSize-1;
i <- 2;
// 인덱스가 힙 크기보다 같거나 커질때 까지 반복
while i <= heapSize do
// 만약 루트 노드가 자식 노드보다 작으면
// 자식 노드 중 가장 큰 노드와 바꾼다
if i < heapSize and A[i] > A[i+1]
then largest <- i
else largest <- i+1
if A[PARENT(largest)] > A[largest]
then break;
A[PARENT(largest)] <-> A[largest]
i <- LEFT(largest);
return root;
힙(Heap) : 구현
앞에서 배운 내용을 토대로 힙 클래스를 구현해보았다.
HeapClass.h
#pragma once
const int MAX_HEAP_NODE = 200;
typedef int NODE;
class HeapClass
{
public:
HeapClass();
~HeapClass();
public:
int IsEmpty();
int IsFull();
NODE Find();
public:
void Initialize();
void Insert(NODE n);
NODE Delete();
void Print();
private:
int Key(NODE n);
NODE Parent(NODE n);
NODE Left(NODE n);
NODE Right(NODE n);
private:
NODE m_Heap[MAX_HEAP_NODE];
int m_heapSize = 0;
};HeapClass.cpp
#include "HeapClass.h"
HeapClass::HeapClass()
{
}
HeapClass::~HeapClass()
{
}
void HeapClass::Initialize()
{
memset(m_Heap, 0, sizeof(NODE) * MAX_HEAP_NODE);
}
int HeapClass::IsEmpty()
{
return (0 == m_heapSize);
}
int HeapClass::IsFull()
{
return (MAX_HEAP_NODE - 1 == m_heapSize);
}
NODE HeapClass::Find()
{
return m_Heap[1];
}
void HeapClass::Insert(NODE n)
{
int i;
if (IsFull())
return;
i = ++(m_heapSize);
while (1 != i && Key(n) > Key(Parent(i)))
{
m_Heap[i] = Parent(i);
i /= 2;
}
m_Heap[i] = n;
}
NODE HeapClass::Delete()
{
NODE root, last;
int parent = 1, child = 2;
if (IsEmpty())
{
cout << "힙 트리 공백에러" << endl;
exit(-1);
}
root = m_Heap[1];
last = m_Heap[m_heapSize--];
while (child <= m_heapSize)
{
if (child < m_heapSize && Key(Left(parent)) < Key(Right(parent)))
++child;
if (Key(last) >= Key(m_Heap[child]))
break;
m_Heap[parent] = m_Heap[child];
parent = child;
child *= 2;
}
m_Heap[parent] = last;
return root;
}
void HeapClass::Print()
{
int level = 1;
for (int i = 1; i <= m_heapSize; ++i)
{
if (level == i)
{
cout << endl;
level *= 2;
}
cout << Key(m_Heap[i]) << ' ' ;
}
cout << "\n-----------";
}
int HeapClass::Key(NODE n)
{
return n;
}
NODE HeapClass::Parent(NODE n)
{
return m_Heap[n / 2];
}
NODE HeapClass::Left(NODE n)
{
return m_Heap[n * 2];
}
NODE HeapClass::Right(NODE n)
{
return m_Heap[n * 2 + 1];
}
main.cpp
#include <iostream>
using namespace std;
#include "HeapClass.h"
int main()
{
HeapClass h;
h.Initialize();
h.Insert(2); h.Insert(5);
h.Insert(4); h.Insert(8);
h.Insert(9); h.Insert(3);
h.Insert(7); h.Insert(3);
h.Print();
h.Delete(); h.Print();
h.Delete(); h.Print();
cout << endl;
}
출력 값

힙 정렬
힙을 이용하여 숫자를 정렬할 숫자들을 Insert하고 차례대로 Delete하여 값을 가져오면 임의의 숫자들을 정렬시킬수 있다.
#include "pch.h"
#include <iostream>
using namespace std;
#include "HeapClass.h"
int main()
{
int data[10];
cout << "정렬 전 : ";
for (int i = 0; i < 10; ++i)
{
data[i] = rand() % 100;
cout << data[i] << " ";
}
cout << "\n";
HeapClass h;
h.Initialize();
for (int i = 0; i < 10; ++i)
{
h.Insert(data[i]);
}
for (int i = 9; i >= 0; --i)
{
data[i] = h.Delete();
}
cout << "정렬 후 : ";
for (int i = 0; i < 10; ++i)
{
cout << data[i] << " ";
}
cout << "\n";
}출력 값

'Data Structure' 카테고리의 다른 글
| 정렬 (Sorting) (0) | 2020.04.10 |
|---|---|
| 그래프 (Graph) (0) | 2020.04.06 |
| 재귀 (Recursion) (0) | 2020.02.29 |
| 이진탐색트리 (Binary search tree) (0) | 2020.02.29 |
| 트리 (Tree) (0) | 2020.02.25 |




