| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 쓰레드
- 멀티프로세서
- 그리디알고리즘
- 락
- 병행성
- 영속성
- 멀티쓰레드
- 백준
- 렌더링 파이프라인
- 다이나믹 프로그래밍
- 알고리즘
- directx
- 다이나믹프로그래밍
- OS
- 디자인패턴
- Direct12
- 자료구조
- 파일시스템 구현
- 운영체제
- 프로그래머스
- 동적계획법
- I/O장치
- 그리디 알고리즘
- 컨디션 변수
- DirectX12
- 병행성 관련 오류
- 스케줄링
- DirectX 12
- 타입 객체
- codility
- Today
- Total
기록공간
동적계획법(Dynamic Programming) 본문
동적계획법 이란?
동적계획법(다이나믹 프로그래밍)은 큰 문제를 작은 문제로 나누어 푸는 알고리즘 방법이다. 다이나믹 프로그래밍이란 명칭은 그냥 알고리즘 창조한 사람이 단지 이름이 멋지다는 이유로 붙여진 것이다(...).
분할정복(Divide and Conquer)과 다른 점
거의 비슷하지만 결정적인 차이점이 존재한다. 그것은 바로 나눠진 작은 문제에서 중복이 일어나는가 안일어나는가이다. 분할정복은 큰 문제를 해결하기 위해 그냥 작은 문제로 나누어 푸는 방법이다. 특징은 작은 문제에서 반복이 일어나는 부분이 없다는 점이다. 동적계획법은 작은 문제들이 반복되는것(단, 바뀌지 않음)을 이용해 풀어나가는 방법이다.
동적계획법의 방법
모든 작은 문제들은 꼭 한번만 풀어야 한다. 그러므로 작은 문제의 정답은 어딘가에 메모해 놓는다. 그리고 그보다 큰 문제를 풀어나갈 때 똑같은 작은 문제가 나타나면 저장했던 값을 사용한다.
동적계획법의 조건
-
같은 문제를 구할 때마다 정답이 같은 경우
-
작은 문제가 반복이 일어나는 경우
위 조건을 만족하는 경우에만 동적프로그래밍을 사용할 수 있다. 작은 문제의 결과 값이 항상 같다는 점을 이용해 큰 문제를 해결하는 방법이기 때문이다.
Memoization?
메모이제이션은 작은 문제들이 반복되고 작은 문제들의 결과값이 항상 같다는 점을 이용하여 한번 계산한 작은 문제를 저장해놓고 다시 사용하는 것이다. 이것을 Memoization이라고 한다.
Ex - 피보나치 수열
피보나치 수열은 1, 1, 2, 3, 5, 8 .. 과 같이 f(n) = f(n - 1) + f(n - 2) (단, n > 2)이라는 점화식을 갖는 순열이다. 재귀 함수로 풀게되면 이보다도 휠씬 간단하게 풀 수 있지만 n이 증가함에 따라 호출되어 쌓이는 함수 메모리와 처리 속도가 기하급수적으로 증가하여 일정 수 이상 넘어가면 시간이 오래걸리거나 메모리 오버플로우로 강제 종료된다.
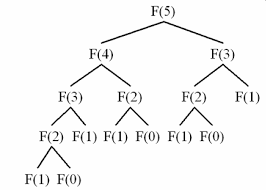
또한 재귀함수로 풀게될 경우, 위 그림처럼 했던 작업을 또 하게 된다. 이런 상황에 동적 계획법을 사용한다. 위에서 살펴본 동적계획법 조건 두가지를 상기하며 풀어보자.
1. 작은 문제들이 반복된다.
F(5)를 구하기 위해서는 F(4), F(3)이 필요하다. 그리고 F(4)를 구하기 위해서는 F(3), F(2)가 필요하다. 두 경우를 살펴보면 F(5)를 구할때도 F(3)이 필요하고 F(4)에서도 F(3)이 필요함을 알 수 있다. 즉, 작은 문제가 반복되는 구조이다.
2. 같은 문제는 항상 정답이 같다.
피보나치 수열의 경우 첫번째와 두번째 수열은 각각 1로 고정되어 있다. 세번째 수열은 언제나 결과값이 2이다. 네번째 수열은 세번째 수열과 두번째 수열을 이용해 구하므로 언제나 정답이 같다는 사실을 알 수 있다.
Memoization
코드로 표현하면 다음과 같다.
#include <iostream>
using namespace std;
int fibonacci(int n)
{
// 중복되는 결과값을 알맞은 위치에 저장할 임시 배열.
int memo[100];
memset(memo, 0, sizeof(int) * 100);
// 1번째 2번째 수열은 값이 1이므로 1을 결과값으로 입력한다.
memo[0] = 1;
memo[1] = 1;
// 3번째 이전에는 값이 1이므로 수열값을 반환한다.
if ((n - 1) < 2)
return memo[n - 1];
// 만약 3번째 이상이라면
// 반복문으로 피보나치 수열을 계산한다.
for (int i = 2; i < n; ++i)
{
// i번째의 결과값을 i번째 메모배열에 저장한다.
// 이전에 계산했던 i - 1번째 i - 2번째 메모를 이용하여
// 수열을 계산한다.
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n - 1];
}n번째 피보나치 수열을 구하는 문제를 동적계획법으로 푼 코드이다. 배열을 이용할 때에는 항상 인덱스에 주의해야 한다.
Bottom-up과 Top_down
Bottom-up
Bottom-up은 작은 문제부터 차근차근 구해나가아가는 방법이다.
int fibonacci_bottom_up(int n)
{
if (n <= 1)
return n;
int first = 0;
int second = 1;
int next = 0;
for (int i = 0; i < n - 1; ++i)
{
next = first + second;
first = second;
second = next;
}
return next;
}
Top-down
재귀함수로 구현하는 경우가 대부분 이 방법이라고 생각하면 된다. 큰 문제를 풀 때 작은 문제가 아직 풀리지 않았다면 그때 작은 문제를 해결하게 된다.
int fibonacci_top_down(int n)
{
int memo[100];
memset(memo, 0, sizeof(int) * 100);
if (memo[n] > 0)
return memo[n];
if (n <= 1)
{
memo[n] = n;
return memo[n];
}
else
{
memo[n] = fibonacci_top_down(n - 1) + fibonacci_top_down(n - 2);
return memo[n];
}
}
Top-down, Bottom-up 뭐가 좋은가?
정답이 없다. 서로 장단점이 있기 때문이다. Top-down은 가독성이 증가된다는 장점이 있지만 작성하기 어렵고, Bottom_up은 풀기는 쉽지만 가독성이 저하될 수 있다. 하지만 둘 중 하나로만 풀리는 문제도 있으니 둘 다 사용법을 알아야 한다.
'Algorithm > 이론' 카테고리의 다른 글
| 크러스컬 알고리즘 (Kruskal Algorithm) (0) | 2020.06.17 |
|---|---|
| 최장증가수열 - LIS(Longest Increasing Subsequence) (0) | 2020.02.17 |
| 너비 우선 탐색 (BFS) (0) | 2020.02.09 |
| 깊이 우선 탐색 (DFS) (0) | 2020.02.09 |
| 그리디 알고리즘 (Greedy Algorithm) (0) | 2020.02.08 |




