| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- I/O장치
- 그리디알고리즘
- 다이나믹프로그래밍
- 스케줄링
- 병행성 관련 오류
- OS
- 멀티프로세서
- 프로그래머스
- DirectX12
- directx
- 렌더링 파이프라인
- 쓰레드
- 자료구조
- DirectX 12
- 컨디션 변수
- 그리디 알고리즘
- Direct12
- 멀티쓰레드
- 운영체제
- 디자인패턴
- 알고리즘
- 동적계획법
- 영속성
- 타입 객체
- 다이나믹 프로그래밍
- 파일시스템 구현
- 락
- 백준
- codility
- 병행성
- Today
- Total
기록공간
최장증가수열 - LIS(Longest Increasing Subsequence) 본문
LIS(최장증가수열)는 동적계획법으로 풀 수 있는 알고리즘 문제 중 하나이다.
어떤 임의의 수열이 주어졌을때, 이 수열에서 몇 개의 수들을 제거해서 부분수열을 만들수 있다.
이 때 만들어진 부분수열 중 오름차순으로 정렬된 가장 긴 수열을 최장증가수열이라고 한다.
예를 들어 다음 수열이 주어졌다고 하자.
3 5 7 9 2 1 4 8
위 수열에서 몇 개의 수를 제거해 부분 수열을 만들었다고 하자.
3 7 9 1 4 8 (5, 2 제거)
7 9 1 8 (3, 5, 2, 4 제거)
3 5 7 8 (9, 2, 1, 4 제거)
1 4 8 (3, 5, 7, 9, 2 제거)
이들 중 세번째와 네번째 수열은 오름차순으로 정렬되어 있다. 이들을 '증가 부분 수열'이라고 한다. 그리고 세번째와 같이 이러한 수열 중 가장 긴 수열을 '최장증가수열(LIS)'이라고 한다.
한 수열에서 여러 개의 LIS가 나올 수도 있다. 예를 들어 수열
5 1 6 2 7 3 8
에서 부분 수열
1 2 3 8
5 6 7 8
은 모두 길이가 4인 LIS이다.
LIS 길이 구하기 문제
첫 번째 알고리즘 : O(N^2)
새로운 배열 D를 정의하자. D[i]의 정의는 다음과 같다.
D[i] : A[i]를 마지막 값으로 가지는 가장 긴 증가부분수열의 길이
A[i]가 어떤 증가부분수열의 마지막 값이 되기 위해서는 A[i]가 추가되기 전 증가부분수열의 마지막 값보다 작은 값이여야 한다. 따라서 A[i]를 마지막 값으로 가지는 '가장 긴' 증가부분수열의 길이는 A[i]가 추가될 수 있는 증가부분수열 중 가장 긴 수열의 길이에 1을 더한 값이 된다.
수열 A = 3 5 7 9 2 1 4 8을 예로 들어 알고리즘을 살펴보자.
(i = 0일 때 A[i] = 0, D[i] = 0이다.)

i = 1일 때를 살펴보자.
A[1] = 3이다. 3은 A[0] = 0 뒤에 붙을 수 있다. 따라서 D[1] = D[0] + 1 = 1 이다.

i = 2일 때를 살펴보자.
A[2] = 5이다. 5는 A[0] = 0, A[1] = 3 뒤에 붙을 수 있다. 이 때 D[0] = 0, D[1] 1에서 D[1]이 가장 크다. 이 말은 A[1] = 3을 가장 마지막 값으로 가지는 LIS의 길이가 가장 길다는 뜻이다. A[2]가 가장 긴 증가부분수열 뒤에 붙는게 더 긴 LIS 뒤에 붙는 게 더 긴 LIS를 만들 수 있다. 따라서 D[2] = D[1] + 1 = 2이다.

i = 3일 때를 살펴보자.
A[3] = 7이다. A[0] = 0, A[1] = 3, A[2] = 5 뒤에 붙을 수 있다. 이 때 D[0] = 0, D[1] = 1, D[2] = 2에서 D[2]가 가장 크다. 따라서 D[3] = D[2] + 1 = 3이다.

i = 4일 떄를 살펴보자.
A[4] = 9이다. 9는 A[0] = 0, A[1] = 3, A[2] = 5, A[3] = 7 뒤에 붙을 수 있다. 이 때 D[0] = 0, D[1] = 1, D[3] = 3에서 D[3]이 가장 크다. 따라서 D[4] = D[3] + 1 = 4이다.
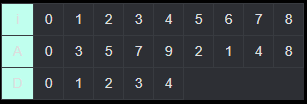
이런 식으로 계속 하다보면 다음과 같이 완성된다.

D의 값들 중 가장 큰 값(D[4] = D[8] = 4)가 이 수열의 LIS 길이이다. 해당 길이를 가지는 부분수열을 찾는 방법은 여러 가지가 있지만, 가장 간단한 것은 해당 값을 가지는 값부터 거꾸로 이어나가는 것이다. 0부터 순서대로 이어나가는 경우는 해당 값을 마지막에 가진다는 보장이 없기 때문이다.
N개의 수들에 대해 자기 자신 전의 모든 수를 다 훑어봐야 하므로 O(N^2)의 시간복잡도를 가지는 알고리즘이 된다.
코드로 표현하면 다음과 같다.
#include <iostream>
using namespace std;
int main()
{
int input = 0;
cin >> input;
int* A = new int[input + 1];
int* D = new int[input + 1];
A[0] = 0;
D[0] = 0;
for (int i = 1; i <= input; ++i)
{
cin >> A[i];
}
for (int i = 1; i <= input; ++i)
{
int max = 0;
for (int j = 0; j < i; ++j)
{
if (A[i] > A[j])
{
if (max < D[j])
max = D[j];
}
}
D[i] = max + 1;
}
for (int i = 1; i <= input; ++i)
{
cout << D[i] << " ";
}
delete[] A;
delete[] D;
}출력 값

두 번째 알고리즘 : O(N log N)
두 번째 알고리즘은 첫 번째 알고리즘을 개량한 형태이다. 두 번째 알고리즘은 다음과 같은 의문에서 시작한다.
`
'D[i]를 계산하기 위해 A[0] ~ A[i - 1]를 꼭 다 훑어봐야 하는가?'
첫 번째 알고리즘에서 A[0] ~ A[i - 1]를 훑어본 것은 A[i]보다 작은 A[j]를 가지는 j들 중 가장 큰 D[j]를 찾기 위함이었다. 여기서 다음과 같은 생각을 이끌어낼 수 있다.
만약 D[j] = k를 만족하는 j 중 A[j]의 값이 가장 작은 j만 어딘가에 저장해 놓으면, 나중에 D[i] (i > j)를 계산 할 때 그 값들만 참조하면 D[i]의 값을 쉽게 알 수 있다.
마찬가지로 수열 A = 3 5 7 9 2 1 4 8을 예로 설명하겠다.

이번에는 하나의 표를 더 생각하자.

이 표는 D[i] = k인 값들 중 A[i]의 값이 가장 작은 값을 계속 저장한다. 이 표의 이름을 X라 하자.
i = 1일 때를 살펴보자.
A[i] = 3이다. 이때 X를 살펴보면 가장 마지막 A[i]의 값이 0이고 이는 3보다 작다. 이 말은 현재 A[1]의 수들로 만든 가장 긴 LIS 중 마지막 값이 0인 LIS가 있다는 말이다. 그리고 A[1]을 그 뒤에 붙일 수 있다. 따라서 D[1] = 0 + 1 = 1이다.

i = 2일 때를 살펴보자
A[2] = 5이다. 이때 X를 살펴보면 가장 마지막 A[i]의 값이 3이고, 이는 5보다 작다 이 말은 현재 A[2] 앞의 수들로 만든 가장 긴 LIS중 마지막 값이 3인 LIS가 있다는 말이다. 그리고 A[2]를 그 뒤에 붙일 수 있다. 따라서 D[2] = 1 + 1 = 2이다.
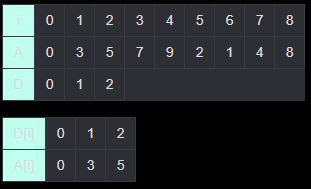
i = 3, 4는 위와 비슷하므로 생략한다.

i = 5일때를 살펴보자.
A[5] = 2이다. 이때 X의 A[i]들을 살펴보면 2는 0과 3사이의 값이다. 그러므로 D[5] = 0 + 1 = 1이다. X에서 D[i] = 1일 때의 A[i] 값은 현재는 3이나, A[5] = 2이므로 더 작은 2로 갱신해준다. 이말은 LIS 길이가 1인 수열 중 끝이 3으로 끝나는 LIS(기존)와 끝이 2로 끝나는 LIS(현재)가 있으므로, 이들 중 끝값이 더 작은 2를 X에 저장해 놓겠다는 것이다. 추후 D[i] = 2인 수열을 찾기 위해 A[5] = 2 뒤에 붙일 수 있는지만 확인하면 되기 때문이다.

이런 식으로 계속 하다보면 다음과 같이 완성된다.

이렇게 해서 배열 D를 완성하였다. D의 값들 중 가장 큰 값(D[4] = D[8] = 4)가 이 수열의 LIS 길이이다.
이 알고리즘은 N개의 수들에 대해 X의 A[i]들을 훑어본다. 이때 X는 오름차순으로 항상 정렬되어 있으므로 이진 탐색을 사용할 수 있다. 이진 탐색을 사용하여 현재 A[i]보다 작은 A[j]를 X에서 찾는다. 그 A[j]에 해당하는 D값에 1를 더해서 D[i]를 쉽게 구할 수 있다. 따라서 이 알고리즘은 O(N log N)의 시간 복잡도를 가진다.
코드로 표현하면 다음과 같다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
// lower_bound 사용을 위해 벡터를 변수로 사용한다.
// vector의 인덱스가 X의 D가 되고,
// vector X의 D인덱스의 값이 X의 A가 된다.
vector<int> vt;
int input = 0;
cin >> input;
int* A = new int[input + 1];
int* D = new int[input + 1];
memset(A, 0, sizeof(int) * (input + 1));
memset(D, 0, sizeof(int) * (input + 1));
// 인덱스 0에 0을 집어 넣어 초기화 해준다.
vt.push_back(0);
for (int i = 1; i <= input; ++i)
{
cin >> A[i];
}
for (int i = 1; i <= input; ++i)
{
// 만약 A[i]가 벡터에 있는 모든 값들보다 큰 경우
// 더 길이가 긴 LIS가 있다는 뜻이므로
// 벡터에 값을 추가한다.
if (vt.back() < A[i])
{
// 가장 뒤에 위치한 값의 인덱스가 D값 이므로
// D[i]의 길이는 그 인덱스 값 + 1 이다.
D[i] = (vt.size() - 1) + 1;
vt.push_back(A[i]);
}
// A[i]가 벡터의 중간에 위치할 수 있는 경우
else
{
// 들어갈 수 있는(또는 A[i]값으로 덮어쓸)
// 적절한 위치를 찾는다.
// lower_bound는 오름차순 정렬이된 컨테이너에서
// 이진 탐색으로 A[i]가 들어갈 수 있는 적절한 위치를
// 이터레이터 형식으로 반환한다.
auto iter = lower_bound(vt.begin(), vt.end(), A[i]);
// 적절한 위치의 인덱스를 구한다.
int dist = distance(vt.begin(), iter);
// 인덱스 위치의 바로 이전 위치의 인덱스값이 X의 D이다.
D[i] = (dist - 1) + 1;
// 인덱스 위치의 값을 A[i]로 덮어쓴다.
vt[dist] = A[i];
}
}
for (int i = 1; i <= input; ++i)
{
cout << D[i] << " ";
}
delete[] A;
delete[] D;
}출력 값은 위와 같다.
이론과 예시에 대한 내용은 나무위키 LIS 문서를 참고하였습니다.
'Algorithm > 이론' 카테고리의 다른 글
| 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2020.06.18 |
|---|---|
| 크러스컬 알고리즘 (Kruskal Algorithm) (0) | 2020.06.17 |
| 동적계획법(Dynamic Programming) (0) | 2020.02.17 |
| 너비 우선 탐색 (BFS) (0) | 2020.02.09 |
| 깊이 우선 탐색 (DFS) (0) | 2020.02.09 |



